- 【問い1】今回は回帰分析の利用に関して誤用と思われる例を示した。これまでのご自身の経験で「(回帰分析に限らず)統計手法の誤用」と感じた事項に出逢ったことがあるか。あれば報告せよ。
- 【問い2】今回、就学援助率と成績の関係を例に、その解釈例を示した。ご自身としてこのデータや解釈例に対してどのように考えるか。自説を述べよ。
===> 公開可とした回答は掲載済み ＆ 参考にどうぞ
- データの重要性、データ解析の注意性。
- 手書きの講義はありがたい。
- 分散の概念の理解にノギス
- 期限前後の入力フォームのコントロール: 設定してみたがうまく機能するだろうか?
- PowerPointのスライド: 同じ内容のスライドは1枚だけを配布資料に入れてある
- 実際の使用例が理解を助ける <===> 数式メインの内容
- 法科大学院の2つの試験。別々の機関が独自に作成。
- 回帰による未来の予測
いくつか(p個)の変量の値を情報の損失をできるだけ少なくして、
少数変量(m個、m＜p)の総合的指標(主成分)で代表させる方法として
主成分分析(Principal Component Analysis, PCA)と
因子分析(Factor Analysis, FA)がある。
いくつかのテストの成績を総合した総合的成績、
いろいろな症状を総合した総合的な重症度、
種々の財務指標に基づく企業の評価
等を求めたいといった場合に用いられる。
p変量(p次元)の観測値をm個(m次元)の主成分に縮約させるという意味で、
次元を減少させる(reduce)方法と言うこともでき、
多変量データを要約する有力な方法である。
両者は似た目的に使われるが、元になっている考え方は異なるので
利用する場面では注意が必要である。違いにも焦点を当てながら説明する。
- 定式化 :
- 変数 :
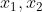
- 重み(係数) :
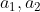
- 合成変量(線形結合) :
-
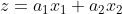
「よく代表する」ように、 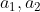を決める。
-
より広がって測定できる軸に沿うと情報量が多い。===> 広がり ===> 分散を最大に
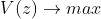(制約条件 : 
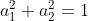の下で)なお、
。
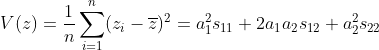ただし、
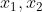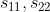[参考:立体の測定: イメージとして] の分散を 
、共分散を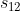 
とする。- ノギスの使い方と寸法の読み取り方: 【通販モノタロウ】
- ノギス :ウィキペディア（Wikipedia）
-
全測定値の分散を最大化する身長と体重(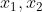)の総合指標 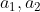を求めよう。
- 求まったベクトルを「軸」とか「主成分」と呼ぶ。
- p次元を何次元に縮約するかの軸数(主成分数)は利用者側が判断する必要がある。
- 主成分の解釈
- 変数 :
- SASプログラム : PCA0501.sas
- 出力結果 : PCA0501-Results.txt,
PCA0501_Output.pdf,
PCA0501_Output.html
- 身長と体重の散布図
- 各変量の平均、標準偏差、分散共分散行列
- 固有値、比率(寄与率)、累積寄与率 : 解釈に使う
- 固有ベクトル(係数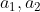) : 解釈に使う
- 主成分得点 : 各個人の得点(z)、2つある
- 第1軸と第2軸の主成分得点の散布図
Sunday, October 31, 2021 05:00:50 PM 30 Plot of shintyou*taijyuu. Legend: A = 1 obs, B = 2 obs, etc. shintyou | | 190 + | | A | A A A | B A A A 180 + A A C C AAAB A | B A BA B A A | ABABA B C BAA AA | A B BA BAAB AA A A | AA AEA A DA 170 + A D CDCED BA A A A A | ADADAABB D | C BAABAAAAA | A C AA A B | A AA B A A A 160 + BCDA AA | AAAAB | A AABAA A | AA A | A A 150 + A | A | B | | 140 + | ---+------------+------------+------------+------------+-- 20 40 60 80 100 taijyuu Sunday, October 31, 2021 05:00:50 PM 31 The PRINCOMP Procedure Observations 199 Variables 2 Simple Statistics shintyou taijyuu Mean 168.8497487 60.44773869 StD 7.9248036 10.50548113 Covariance Matrix shintyou taijyuu shintyou 62.8025126 56.7763504 taijyuu 56.7763504 110.3651337 Total Variance 173.16764631 Eigenvalues of the Covariance Matrix Eigenvalue Difference Proportion Cumulative 1 148.139527 123.111408 0.8555 0.8555 2 25.028119 0.1445 1.0000 Sunday, October 31, 2021 05:00:50 PM 32 The PRINCOMP Procedure Eigenvectors Prin1 Prin2 shintyou 0.553923 0.832568 taijyuu 0.832568 -.553923 Sunday, October 31, 2021 05:00:51 PM 33 s h t k c i a j o a t n i k i d r s P P t j y t u r u r r O s y y o a k y u i i b e o u u k a e w n n s x u u i u i r a 1 2 1 F 145.5 42.0 76 自宅生 0 3700 -28.2930 -9.2216 2 F 146.7 41.0 85 自宅生 10000 Vodafone 6000 -28.4608 -7.6686 3 F 148.0 43.0 80 自宅生 50000 DoCoMo 4000 -26.0756 -7.6941 4 F 150.0 46.0 86 40000 . -22.4700 -7.6908 5 F 151.7 41.5 80 自宅生 35000 . -25.2749 -3.7827 6 F 152.0 35.0 77 自宅生 60000 DoCoMo 2000 -30.5204 0.0675 7 F 153.0 46.5 87 下宿生 10000 . -20.3920 -5.4700 8 F 153.0 55.0 78 自宅生 30000 . -13.3152 -10.1784 9 F 154.4 44.0 75 自宅生 9000 au 2000 -21.6979 -2.9196 10 F 155.0 48.0 83 下宿生 180000 . -18.0353 -4.6358 11 F 156.0 42.0 85 自宅生 0 DoCoMo 15000 -22.4768 -0.4797 12 F 156.0 46.0 82 自宅生 10000 Vodafone 7000 -19.1465 -2.6953 13 F 156.0 48.0 70 自宅生 30000 . -17.4814 -3.8032 14 F 156.0 49.0 85 自宅生 25000 . -16.6488 -4.3571 15 F 156.0 50.0 82 自宅生 40000 Vodafone 10000 -15.8162 -4.9110 Sunday, October 31, 2021 05:00:51 PM 34 Plot of Prin2*Prin1. Legend: A = 1 obs, B = 2 obs, etc. 20 + | | | | | | | | | | A| A | | A A 10 + | C | A A|AAAA AA | AA C A Prin2 | A A A A | B B A | B AA BA | B B AA | AA B CABB B| A B AAAA AA | A B A AB A CBBB A AA A AA 0 +---------A------A----AA---A--BA--A-A-DA---A--B-A----------------------- | A AACCA A A AB ABABBACA A A A | A A B B A A| B AA BBB A A A | A BAA A A A B A A A A | A A A | A A | A A A A A AA A A A | A | A -10 + A | A A | A | A | | A | | A | | A | | | | -20 + | --+----------------+----------------+----------------+----------------+- -40 -20 0 20 40 Prin1 - 解釈方法
- 寄与率(Proportion) : その軸がどの程度説明力を持っているか :
- 第1軸だけで十分(85.6%)。第2軸に含まれる説明力は小さい(14.5%)。
- 固有ベクトル(Eigenvectors) : その軸の特徴を示している :
- 身長と体重の重みはほぼ同等(0.6と0.8)だが、体重がやや大きめに効いている(第1軸)
- 主成分得点と散布図 : 各個人がどこに付置されているか
- 第1軸 : 全体的な体格の指標。身長と体重を足したような指標。
- ちなみに第2軸 : 全体的な体格の指標だが、体重が負に効く。
- 元の散布図が回転していることが判るであろうか?
- 回転の中心点はそれぞれの変量の平均値。
- 寄与率(Proportion) : その軸がどの程度説明力を持っているか :
-
定式化 :
- 2変量の時の考え方を拡張したもの(p変量)
-
合成変量(線形結合) :
-
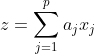
より広がって測定できる軸に沿うと情報量が多い。===> 広がり ===> 分散を最大に
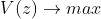(制約条件 :
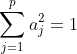の下で) -
合成変量の分散を最大化する軸を決定する。
-
よく代表するように、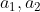,… を決める。
-
身長、体重、胸囲での総合指標を求めてみよう :
- SASプログラム : PCA0502.sas
- 出力結果 : PCA0502-Results.txt,
PCA0502_Output.pdf,
PCA0502_Output.html
- 各変量の平均、標準偏差、共分散行列
- 固有値、比率(寄与率)、累積寄与率
- 固有ベクトル
- 主成分得点
- 第1軸～第3軸の散布図
Sunday, October 31, 2021 03:26:02 PM 59 The PRINCOMP Procedure Observations 199 Variables 3 Simple Statistics shintyou taijyuu kyoui Mean 168.8497487 60.44773869 86.34221106 StD 7.9248036 10.50548113 8.88626378 Covariance Matrix shintyou taijyuu kyoui shintyou 62.8025126 56.7763504 20.7993036 taijyuu 56.7763504 110.3651337 47.7707020 kyoui 20.7993036 47.7707020 78.9656840 Total Variance 252.13333029 Eigenvalues of the Covariance Matrix Eigenvalue Difference Proportion Cumulative 1 175.540573 121.609468 0.6962 0.6962 2 53.931105 31.269454 0.2139 0.9101 3 22.661651 0.0899 1.0000 Sunday, October 31, 2021 03:26:02 PM 60 The PRINCOMP Procedure Eigenvectors Prin1 Prin2 Prin3 shintyou 0.464556 -.478107 0.745387 taijyuu 0.749904 -.235289 -.618290 kyoui 0.470991 0.846199 0.249230 Sunday, October 31, 2021 03:26:03 PM 61 s h t k c i a j o a t n i k i d r s P P P t j y t u r u r r r O s y y o a k y u i i i b e o u u k a e w n n n s x u u i u i r a 1 2 3 1 F 145.5 42.0 76 自宅生 0 3700 -29.5524 6.7527 -8.5761 2 F 146.7 41.0 85 自宅生 10000 Vodafone 6000 -25.5059 14.0300 -4.8203 3 F 148.0 43.0 80 自宅生 50000 DoCoMo 4000 -25.7571 8.7069 -6.3340 4 F 150.0 46.0 86 40000 . -19.7523 12.1220 -5.2027 5 F 151.7 41.5 80 自宅生 35000 . -25.1631 7.2908 -2.6487 6 F 152.0 35.0 77 自宅生 60000 DoCoMo 2000 -31.3111 6.1382 0.8462 7 F 153.0 46.5 87 下宿生 10000 . -17.5127 11.4163 -3.0265 8 F 153.0 55.0 78 自宅生 30000 . -15.3775 1.8005 -10.5250 9 F 154.4 44.0 75 自宅生 9000 au 2000 -24.3890 1.1807 -3.4280 10 F 155.0 48.0 83 下宿生 180000 . -17.3427 6.7223 -3.4601 11 F 156.0 42.0 85 自宅生 0 DoCoMo 15000 -20.4356 9.3483 1.4935 12 F 156.0 46.0 82 自宅生 10000 Vodafone 7000 -18.8490 5.8686 -1.7273 13 F 156.0 48.0 70 自宅生 30000 . -23.0011 -4.7564 -5.9547 14 F 156.0 49.0 85 自宅生 25000 . -15.1863 7.7013 -2.8345 15 F 156.0 50.0 82 自宅生 40000 Vodafone 10000 -15.8494 4.9274 -4.2005 Sunday, October 31, 2021 03:26:03 PM 62 Plot of Prin2*Prin1. Legend: A = 1 obs, B = 2 obs, etc. 20 + | | | A | A | A A A | A A | A | B A A A A AB | AA A A | AA AABCD A BAB| AAAB A A | AABAAABB DB CAC E A AAB AA A A 0 +-----------A----A--DA--BBBBC+BBD-ADCAA-AA-ABAA------------------------- | A A ABA AC E D DCBAA AA | A A A BBAA BB AAA AA A Prin2 | A AA BA A A | AA A| A A A A | A | | A | -20 + | | A | | | | | | | | | | | -40 + | | A | | | A | | | | | | | -60 + | -+-------------+-------------+-------------+-------------+-------------+ -40 -20 0 20 40 60 Prin1 Sunday, October 31, 2021 03:26:03 PM 63 Plot of Prin3*Prin2. Legend: A = 1 obs, B = 2 obs, etc. Prin3 | | | | 20 + | | | | | | | | A| 10 + A A A B | | A A BB | | ABB B B A|AB A | A A AC CBBCA ABA | BBACCDHEBD AA A A 0 +---------------------------------A---A--AAA-B---AAADGAAADC-B----A-A---- | A B BBCCCADBBADB A | A B A AEABBA BC AA A B | AA AAA A A A A | A A A -10 + | A A A | | A | A A | | A | | -20 + | | A | | | | | | | -30 + | | | -+---------+---------+---------+---------+---------+---------+---------+ -50 -40 -30 -20 -10 0 10 20 Prin2 Sunday, October 31, 2021 03:26:03 PM 64 Plot of Prin3*Prin1. Legend: A = 1 obs, B = 2 obs, etc. Prin3 | | | | 20 + | | | | | | | | | A 10 + A A| B A | A AAA B | A A DB AAA AAA | A AA B AABA AAA A BAA BA | A A AAAA DBBACBABD BBAA AB A A 0 +------A--------BA-ACBBAAB-BA+AAD-AA-C-CA--A---------------------------- | A ABAABBA AB D|ACACAAAA A A A | AA AABA B A B |ABAA ABAB A A A | A A A A A |A A A A | A | A A -10 + A A | A | | A | A | A | | A | | -20 + | | A | | | | | | -30 + | | | -+-------------+-------------+-------------+-------------+-------------+ -40 -20 0 20 40 60 Prin1 - 解釈方法
- 寄与率 : 2軸まで取れば十分のようだ(累積の項 91.0%)。
- 各軸の意味付け
- 第1軸 : 全体的な体格の因子。特に体重が効いている。
- 第2軸 : 太さの因子(?)。胸囲が正で大きく、身長が負。
- ちなみに、第3軸 : 華奢さの因子(?)。無視しても良い軸であるが。(9.0%)。
- 変量によって測定単位が異なる
- 使う単位によって解析結果が異なる
- 分散の影響を受ける
- 各変量を標準化して用いる : 相関行列 <===> 分散共分散行列
- 相関行列を用いて体格の総合指標を求めてみよう :
- SASプログラム : PCA0503.sas
- 出力結果 : PCA0503-Results.txt,
PCA0503_Output.pdf,
PCA0503_Output.html
- 各変量の平均、標準偏差、相関行列
- 固有値、比率(寄与率)、累積寄与率
- 固有ベクトル
- 主成分得点
- 第1軸～第3軸の散布図
Sunday, October 31, 2021 03:26:46 PM 77 The PRINCOMP Procedure Observations 199 Variables 3 Simple Statistics shintyou taijyuu kyoui Mean 168.8497487 60.44773869 86.34221106 StD 7.9248036 10.50548113 8.88626378 Correlation Matrix shintyou taijyuu kyoui shintyou 1.0000 0.6820 0.2954 taijyuu 0.6820 1.0000 0.5117 kyoui 0.2954 0.5117 1.0000 Eigenvalues of the Correlation Matrix Eigenvalue Difference Proportion Cumulative 1 2.00917168 1.28938921 0.6697 0.6697 2 0.71978247 0.44873662 0.2399 0.9097 3 0.27104585 0.0903 1.0000 Sunday, October 31, 2021 03:26:46 PM 78 The PRINCOMP Procedure Eigenvectors Prin1 Prin2 Prin3 shintyou 0.581024 -.562895 0.587844 taijyuu 0.644596 -.122703 -.754613 kyoui 0.496898 0.817370 0.291546 - 解釈方法
- 寄与率 : 2軸まで取れば十分のようだ(累積の項 91.0%)。
- 各軸の意味付け
- 第1軸 : 全体的な体格の因子。
- 第2軸 : 太さの因子。
- [今回の例では] 分散共分散行列を使ったときよりも 第1軸の固有ベクトル同士が近い値になった。しかし、軸の解釈に違いはない。 劇的に変化したら両者の違いが明確になって説得力を増したのであろうが、 その点では残念である。 このように近い値になった理由は、この例では 3変量のスケールや分散に それほどの違いがないためと思われる。
【参考】分散共分散行列と相関行列を使ったときの違いを見てみたければ、 shintyou のみを mm 単位で測定したと仮定して、 10倍したものをデータとして両者の出力を比較してみよ。
- SASプログラム : PCA0504.sas
- 出力結果 : PCA0504-Results.txt, PCA0504_Output.pdf, PCA0504_Output.html
明確に決まっているわけではないが、以下のような基準が一般的に
用いられている。また、結果の解釈の都合上、多少増減させることもある。
- 累積寄与率がある程度(例えば80%以上)以上大きくなること
- 固有値のギャップがある程度以上大きいこと
- 相関行列を用いている場合、固有値が 1以上
- ...
[ノウハウ] 軸の特性を把握するにはラインマーカーが重宝する。 一つの軸内で大きい(もしくは小さい)固有ベクトルにマークすると、 何がグルーピングされているかが理解し易くなる。 ただ、今週の例示では3軸までしか出現しないので、ご利益は感じにくいとも思う。 多変量(例えば以下の食品の嗜好性データ(PCA/FAとも))になればその有効性が理解できるであろう。
100種類の食品(ごはん、お茶漬け、…、リンゴ、パイ缶)に対する 性・年齢で分割した10グループの嗜好度調査のデータをMoodleに掲載しておく。 グループ1から5は男性、グループ6から10は女性であり、その中の番号の小さい方から順に 15才以下、16～20才以下、21～30才以下、31～40才以下、41才以上の10群を構成している。 また、測定尺度は「1: おらく食べる気がしない」、「2: もし強制されれば食べる」、…、 「8: いつも食べたい」、「9: もっとも好きな食品に入る」までの9段階であり、 各グループごとに尺度の平均値を取ったものが測定値として格納されている。
- 食品嗜好度調査データの説明文、 データ : food.dat
- 相関行列を用いて総合指標を求めてみよう :
- SASプログラム : PCA0505.sas
- 出力結果 : PCA0505-Results.txt,
PCA0505_Output.pdf,
PCA0505_Output.html
Sunday, October 31, 2021 03:28:00 PM 124 Obs X01 X02 X03 X04 X05 X06 X07 X08 X09 X10 1 7.69 7.31 7.47 7.76 7.87 7.51 7.24 7.70 7.91 7.95 2 6.59 5.56 6.21 6.04 5.81 6.64 6.11 6.53 6.44 6.64 3 4.55 4.18 4.36 4.25 4.53 4.60 3.66 4.04 3.68 4.43 4 6.78 6.11 6.30 5.98 5.56 6.37 6.29 5.43 5.32 5.28 5 6.47 6.24 6.02 5.42 5.88 6.00 5.60 4.60 5.40 5.95 6 6.96 6.81 6.91 6.48 6.23 7.09 7.27 7.13 6.86 7.36 7 6.57 5.70 5.89 5.16 5.30 6.07 5.56 4.50 4.92 5.33 8 7.32 6.95 6.02 4.98 4.88 6.82 6.40 5.53 5.61 5.33 9 6.51 6.15 5.51 4.68 4.16 5.17 4.81 4.70 4.86 3.82 10 6.86 6.05 5.85 6.14 6.75 6.71 5.39 5.42 6.03 6.59 Sunday, October 31, 2021 03:28:00 PM 125 The PRINCOMP Procedure Observations 100 Variables 10 Simple Statistics X01 X02 X03 X04 X05 Mean 6.038100000 5.784800000 5.947100000 5.669500000 5.640600000 StD 1.239147389 1.034139939 0.825972699 0.915395124 0.884228614 Simple Statistics X06 X07 X08 X09 X10 Mean 5.781300000 5.563900000 5.379400000 5.517400000 5.542100000 StD 1.294327683 1.182607883 1.121124814 1.016264322 1.130856737 Correlation Matrix X01 X02 X03 X04 X05 X01 M(-15) 1.0000 0.8708 0.5158 0.3701 0.1723 X02 M(16-20) 0.8708 1.0000 0.7588 0.6043 0.4021 X03 M(21-30) 0.5158 0.7588 1.0000 0.8524 0.7262 X04 M(31-40) 0.3701 0.6043 0.8524 1.0000 0.8742 X05 M(41-) 0.1723 0.4021 0.7262 0.8742 1.0000 X06 F(-15) 0.9384 0.8207 0.5164 0.3580 0.2077 X07 F(16-20) 0.8107 0.8381 0.6584 0.4875 0.3543 X08 F(21-30) 0.6161 0.7095 0.6990 0.6199 0.5235 X09 F(31-40) 0.5003 0.6470 0.7013 0.7207 0.7101 X10 F(41-) 0.3298 0.4569 0.5584 0.6321 0.7479 Sunday, October 31, 2021 03:28:00 PM 126 The PRINCOMP Procedure Correlation Matrix X06 X07 X08 X09 X10 X01 0.9384 0.8107 0.6161 0.5003 0.3298 X02 0.8207 0.8381 0.7095 0.6470 0.4569 X03 0.5164 0.6584 0.6990 0.7013 0.5584 X04 0.3580 0.4875 0.6199 0.7207 0.6321 X05 0.2077 0.3543 0.5235 0.7101 0.7479 X06 1.0000 0.8888 0.7465 0.6215 0.4932 X07 0.8888 1.0000 0.8949 0.7679 0.6415 X08 0.7465 0.8949 1.0000 0.8528 0.7741 X09 0.6215 0.7679 0.8528 1.0000 0.9112 X10 0.4932 0.6415 0.7741 0.9112 1.0000 Eigenvalues of the Correlation Matrix Eigenvalue Difference Proportion Cumulative 1 6.82795512 5.06608201 0.6828 0.6828 2 1.76187311 1.00742187 0.1762 0.8590 3 0.75445124 0.49207487 0.0754 0.9344 4 0.26237637 0.14082435 0.0262 0.9607 5 0.12155202 0.02358655 0.0122 0.9728 6 0.09796547 0.02586580 0.0098 0.9826 7 0.07209967 0.02801926 0.0072 0.9898 8 0.04408041 0.00832792 0.0044 0.9942 9 0.03575249 0.01385842 0.0036 0.9978 10 0.02189408 0.0022 1.0000 Sunday, October 31, 2021 03:28:00 PM 127 The PRINCOMP Procedure Eigenvectors Prin1 Prin2 Prin3 Prin4 Prin5 X01 M(-15) 0.286033 -.446335 0.193512 0.428019 0.162365 X02 M(16-20) 0.331337 -.239842 0.336063 0.022488 -.559594 X03 M(21-30) 0.323345 0.166337 0.442291 -.436029 -.168594 X04 M(31-40) 0.299329 0.358627 0.375366 0.063449 0.367912 X05 M(41-) 0.260727 0.507209 0.127419 0.375425 0.146879 X06 F(-15) 0.308635 -.407882 -.083695 0.267375 0.286866 X07 F(16-20) 0.344271 -.252697 -.171400 -.295655 -.025050 X08 F(21-30) 0.347877 -.032314 -.289087 -.507508 0.452377 X09 F(31-40) 0.345636 0.164368 -.322236 0.040012 -.388944 X10 F(41-) 0.303334 0.267273 -.522559 0.251270 -.190507 Eigenvectors Prin6 Prin7 Prin8 Prin9 Prin10 X01 -.016413 -.062138 -.038493 -.141617 0.668052 X02 -.212367 0.479465 0.283325 -.013739 -.225064 X03 0.476929 -.416354 0.136150 0.085922 0.163960 X04 -.562491 -.066245 -.114301 0.403713 -.068344 X05 0.385123 0.325310 -.167534 -.437833 -.148648 X06 0.209878 -.335058 0.176137 0.090538 -.618107 X07 0.137469 0.236104 -.762654 0.204382 -.046351 X08 -.128390 0.256135 0.382983 -.303270 0.106863 X09 -.387189 -.488821 -.161974 -.425188 -.030381 X10 0.181955 0.100632 0.270185 0.543107 0.229904 Sunday, October 31, 2021 03:28:00 PM 128 Obs X01 X02 X03 X04 X05 X06 X07 X08 X09 X10 Prin1 Prin2 1 7.69 7.31 7.47 7.76 7.87 7.51 7.24 7.70 7.91 7.95 5.88693 1.44204 2 6.59 5.56 6.21 6.04 5.81 6.64 6.11 6.53 6.44 6.64 1.65842 0.13686 3 4.55 4.18 4.36 4.25 4.53 4.60 3.66 4.04 3.68 4.43 -4.44537 -0.34692 4 6.78 6.11 6.30 5.98 5.56 6.37 6.29 5.43 5.32 5.28 0.72138 -0.63217 5 6.47 6.24 6.02 5.42 5.88 6.00 5.60 4.60 5.40 5.95 0.15339 -0.18363 6 6.96 6.81 6.91 6.48 6.23 7.09 7.27 7.13 6.86 7.36 3.65322 0.09908 7 6.57 5.70 5.89 5.16 5.30 6.07 5.56 4.50 4.92 5.33 -0.65902 -0.78995 8 7.32 6.95 6.02 4.98 4.88 6.82 6.40 5.53 5.61 5.33 0.76044 -1.96919 9 6.51 6.15 5.51 4.68 4.16 5.17 4.81 4.70 4.86 3.82 -1.96687 -1.71968 10 6.86 6.05 5.85 6.14 6.75 6.71 5.39 5.42 6.03 6.59 1.35649 0.51749 11 7.04 6.03 6.53 6.02 6.68 6.78 5.91 6.26 5.76 5.95 1.76317 0.15476 12 6.59 6.30 6.29 5.94 6.10 5.93 5.52 5.35 5.45 5.85 0.72383 0.14551 13 5.93 4.76 5.09 5.51 5.79 5.49 4.97 4.69 5.30 5.61 -1.20892 0.34668 14 7.00 6.31 6.82 6.26 5.26 6.69 6.27 5.94 5.78 5.26 1.42272 -0.75706 15 6.63 5.47 5.54 4.88 4.70 5.89 4.64 4.43 4.00 3.98 -2.13183 -1.49511 Obs Prin3 Prin4 Prin5 Prin6 Prin7 Prin8 Prin9 Prin10 1 -0.07682 0.40809 0.25348 -0.08404 0.00629 0.07518 -0.29432 0.07804 2 -0.90098 -0.05516 0.42231 -0.06712 -0.42537 0.15924 0.03126 0.21633 3 -0.55169 0.23782 0.37097 0.08301 0.22924 0.36927 0.13546 -0.13545 4 0.55357 -0.08449 0.21583 0.10836 -0.04069 -0.30130 0.23414 0.03747 5 0.21693 0.67993 -0.55569 0.43975 0.12407 -0.03449 0.20098 0.03292 6 -0.63902 -0.35301 -0.06665 0.08296 0.01967 0.09429 0.27099 0.10991 7 0.26301 0.42015 -0.16052 0.48267 -0.13359 -0.13508 0.28383 0.14238 8 0.06701 -0.04720 -0.60733 0.05720 0.07830 0.10980 -0.04606 0.07099 9 0.66740 -0.33431 -0.54215 -0.50605 -0.09164 0.28167 -0.34880 0.33721 10 -0.17674 1.31452 0.21057 0.17171 0.08563 0.18324 -0.13665 -0.09062 11 0.23456 0.33063 0.60092 0.58481 0.05801 0.16376 -0.43135 0.07070 12 0.49777 0.35538 -0.09548 0.21636 0.19362 0.18252 0.04441 0.14858 13 -0.53251 0.85212 0.41764 -0.06351 -0.06122 -0.26835 -0.02047 0.09838 14 0.71704 -0.53272 0.19744 -0.12540 -0.54510 0.00683 0.21138 0.12406 15 0.88751 0.23480 0.36191 0.24293 -0.09797 0.25997 0.00113 0.14547 Sunday, October 31, 2021 03:28:00 PM 129 Plot of Prin2*Prin1. Legend: A = 1 obs, B = 2 obs, etc. 4 + | | | | | | | | | | A A| | |A A 2 + A | A A A | A A A A | |A A A A Prin2 | A A A B| A A | A B AA A| A A | A A A A AA A A B | A A A A A | A A A A 0 +----------------------------------A----A+--A----A---A-----AA-------A--- | A A |A A A | A A A | A BA A | A A | A B AA | A | A A | A | A A A | A A A | A A -2 + A A A| A | A | A A | A | | | A | | | | | A | -4 + | -+---------+---------+---------+---------+---------+---------+---------+ -8 -6 -4 -2 0 2 4 6 Prin1 Sunday, October 31, 2021 03:28:00 PM 130 Plot of Prin3*Prin2. Legend: A = 1 obs, B = 2 obs, etc. Prin3 | | | | 3 + | | | A | | | | A | A | A 2 + | A | | A | | A | | AA | A | 1 + | AA | AA AAA | | A A A | A | A A |A A | A A A A AA BBA AA A A AA A A 0 +-------------------AA-A-A-A-------------+-------------A---------------- | A A AAA | A AA A | A A A A A A A AA | A A B |B A A A A B A | B A | A A A -1 + A AAA B A A | | | | A A A | | AA | | -2 + | | | -+---------+---------+---------+---------+---------+---------+---------+ -4 -3 -2 -1 0 1 2 3 Prin2 Sunday, October 31, 2021 03:28:00 PM 131 Plot of Prin1*Prin3. Legend: A = 1 obs, B = 2 obs, etc. Prin1 | | | | 7.5 + | | | | | | A A| 5.0 + A A | | A A | A A | A | A | A A 2.5 + A A A | AAA A | B A A A A A A A | A A AB | AB B | A A A A AA AA AA A 0.0 +---------A----A-A--AAA---A-A+--BA-------------A------------------------ | A A | A A | A A | A A | A A | A A A A A -2.5 + A A A A C A | B A | AA | A A | BA | | A | -5.0 + | A | A A | A | | | | A -7.5 + | | | -+-------------+-------------+-------------+-------------+-------------+ -2 -1 0 1 2 3 Prin3--> - 解釈方法
- 寄与率 : 2軸まで取れば十分のようではある(累積の項 85.9%)。
- 一方で、固有値の変化量からすると、3軸でも良さそう : 3と4の間が空いてるから
- そこで、主成分の数を3として意味付けを考えてみよう
- 各軸の意味付け: 参考までに食品番号でプロットしてみると。
- 第1軸 : 全体的な嗜好度合い。
- 第2軸 : 年齢による嗜好度合い(若いとマイナス)。
- 第3軸 : 性別による嗜好度合い(男性だとプラス)。
上述の主成分分析の場合は、
データの散らばり方(分散)を捉えてデータ特性を把握する手法であった。
一方、因子分析は、変数間に(潜在的な)構造を持ち込んで関係を探る手法である
(少し理解しにくいかもしれないが)。
この手法は心理学の分野で広く利用されている。
- 定式化
-
例えば、i番目の学生の3科目の試験成績
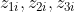が得られていたとする(i=1,2,…,n)。 fiをi番目の学生の特徴を表す要素、ajをj番目の科目の特徴を表す要素とし、 それらが以下のような積の形で表現できたとしたら、学生個人と科目の特性が分離できることになる。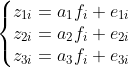
-
-
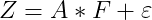
ここで、
-
測定対象
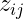: 成績、測定値、…。
-
共通因子(潜在変量) :
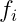: 因子得点(測定できない潜在変量)、個体の特徴付け、i=1,2,3,…,n.
-
因子負荷量(潜在変量) :
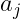: 因子の特徴付け、j=1,2,3,…,p.
-
独自因子 :
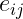: 変動、誤差
-
測定対象
-
いくつかの仮定 : 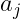, , 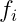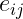の下で、これらを満たす 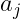, 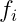を求める。
-
回転の不定性:
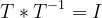となる回転行列Tを用いると、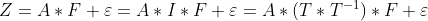
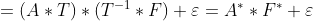
となり、AとFの対は無限組存在する。一意には決まらない。 何らかの基準を条件に確定させる。
-
-
p次元を何次元に縮約するかの軸数(因子数)も利用者側から与える必要がある。
- 因子の解釈
- 因子軸の回転 : 直交回転、斜交回転
- 因子数を指定して分析を進める必要があるため、 前処理や確定した因子数に基づく分析等、 行きつ戻りつの試行錯誤が必要な手法である。
- まずは因子数を決めよう
-
固有値(Eigenvalue) : 相関行列の固有値の振る舞いから因子数(軸数)を決める。
- 因子数の決定 : 解析者側の判断
- 固有値の大小、減少傾向から因子数を決める。
- 因子数の決め方は、主成分分析の時と同様の考え方
- 累積寄与率(Cumulative)
- 固有値の値(Eigenvalue, Proportion)
- 固有値間のギャップ(Difference) 等
-
固有値(Eigenvalue) : 相関行列の固有値の振る舞いから因子数(軸数)を決める。
- SASプログラム : FA0611.sas
- 出力結果 : FA0611-Results.txt,
FA0611_Output.pdf,
FA0611_Output.html
Monday, November 1, 2021 09:36:28 PM 5 Obs X01 X02 X03 X04 X05 X06 X07 X08 X09 X10 1 7.69 7.31 7.47 7.76 7.87 7.51 7.24 7.70 7.91 7.95 2 6.59 5.56 6.21 6.04 5.81 6.64 6.11 6.53 6.44 6.64 3 4.55 4.18 4.36 4.25 4.53 4.60 3.66 4.04 3.68 4.43 4 6.78 6.11 6.30 5.98 5.56 6.37 6.29 5.43 5.32 5.28 5 6.47 6.24 6.02 5.42 5.88 6.00 5.60 4.60 5.40 5.95 6 6.96 6.81 6.91 6.48 6.23 7.09 7.27 7.13 6.86 7.36 7 6.57 5.70 5.89 5.16 5.30 6.07 5.56 4.50 4.92 5.33 8 7.32 6.95 6.02 4.98 4.88 6.82 6.40 5.53 5.61 5.33 9 6.51 6.15 5.51 4.68 4.16 5.17 4.81 4.70 4.86 3.82 10 6.86 6.05 5.85 6.14 6.75 6.71 5.39 5.42 6.03 6.59 Monday, November 1, 2021 09:36:28 PM 6 The FACTOR Procedure Input Data Type Raw Data Number of Records Read 100 Number of Records Used 100 N for Significance Tests 100 Monday, November 1, 2021 09:36:28 PM 7 The FACTOR Procedure Initial Factor Method: Principal Components Prior Communality Estimates: ONE Eigenvalues of the Correlation Matrix: Total = 10 Average = 1 Eigenvalue Difference Proportion Cumulative 1 6.82795512 5.06608201 0.6828 0.6828 2 1.76187311 1.00742187 0.1762 0.8590 3 0.75445124 0.49207487 0.0754 0.9344 4 0.26237637 0.14082435 0.0262 0.9607 5 0.12155202 0.02358655 0.0122 0.9728 6 0.09796547 0.02586580 0.0098 0.9826 7 0.07209967 0.02801926 0.0072 0.9898 8 0.04408041 0.00832792 0.0044 0.9942 9 0.03575249 0.01385842 0.0036 0.9978 10 0.02189408 0.0022 1.0000 2 factors will be retained by the MINEIGEN criterion. Monday, November 1, 2021 09:36:28 PM 8 The FACTOR Procedure Initial Factor Method: Principal Components Factor Pattern Factor1 Factor2 X01 M(-15) 0.74741 -0.59244 X02 M(16-20) 0.86579 -0.31836 X03 M(21-30) 0.84491 0.22079 X04 M(31-40) 0.78216 0.47602 X05 M(41-) 0.68129 0.67325 X06 F(-15) 0.80647 -0.54140 X07 F(16-20) 0.89959 -0.33542 X08 F(21-30) 0.90901 -0.04289 X09 F(31-40) 0.90316 0.21817 X10 F(41-) 0.79262 0.35477 Variance Explained by Each Factor Factor1 Factor2 6.8279551 1.7618731 Final Communality Estimates: Total = 8.589828 X01 X02 X03 X04 X05 0.90961791 0.85094991 0.76262367 0.83837129 0.91741340 X06 X07 X08 X09 X10 0.94352040 0.92177476 0.82814690 0.86329813 0.75411185 - 解釈方法 : 軸の数を決めることがメイン。軸の特徴の解釈がメインではない。
- 固有値(Eigenvalue) : 相関行列を用いた主成分分析の計算結果
- 相関行列を用いた主成分が計算される (因子数を決めるため)
- [コメント] 理解を難しくしている一つの理由かもしれない
- システム側からは因子数は2だと判断された : 固有値が1より大きい
- 因子負荷量(Factor Pattern) :
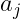
- 因子毎の分散(Variance explained by each factor) : 総分散(10, 変量数と等しくなる)のどれだけを説明しているか。因子毎の説明量。
- 共通性(Final Communality Estimates, Σaj^2) : 変数毎の説明割合。
- 因子数の決定 : 解析者側の判断
- 固有値の変化量からすると、3 でも良さそう : 3 と 4 の間が空いてる
- 因子数を 3 として計算してみよう
- 固有値(Eigenvalue) : 相関行列を用いた主成分分析の計算結果
- SASプログラム : FA0612.sas
- 出力結果 : FA0612-Results.txt,
FA0612_Output.pdf,
FA0612_Output.html
Monday, November 1, 2021 09:37:03 PM 10 The FACTOR Procedure Input Data Type Raw Data Number of Records Read 100 Number of Records Used 100 N for Significance Tests 100 Monday, November 1, 2021 09:37:03 PM 11 The FACTOR Procedure Initial Factor Method: Principal Components Prior Communality Estimates: ONE Eigenvalues of the Correlation Matrix: Total = 10 Average = 1 Eigenvalue Difference Proportion Cumulative 1 6.82795512 5.06608201 0.6828 0.6828 2 1.76187311 1.00742187 0.1762 0.8590 3 0.75445124 0.49207487 0.0754 0.9344 4 0.26237637 0.14082435 0.0262 0.9607 5 0.12155202 0.02358655 0.0122 0.9728 6 0.09796547 0.02586580 0.0098 0.9826 7 0.07209967 0.02801926 0.0072 0.9898 8 0.04408041 0.00832792 0.0044 0.9942 9 0.03575249 0.01385842 0.0036 0.9978 10 0.02189408 0.0022 1.0000 3 factors will be retained by the NFACTOR criterion. Monday, November 1, 2021 09:37:03 PM 12 The FACTOR Procedure Initial Factor Method: Principal Components Factor Pattern Factor1 Factor2 Factor3 X01 M(-15) 0.74741 -0.59244 0.16808 X02 M(16-20) 0.86579 -0.31836 0.29190 X03 M(21-30) 0.84491 0.22079 0.38417 X04 M(31-40) 0.78216 0.47602 0.32604 X05 M(41-) 0.68129 0.67325 0.11067 X06 F(-15) 0.80647 -0.54140 -0.07270 X07 F(16-20) 0.89959 -0.33542 -0.14888 X08 F(21-30) 0.90901 -0.04289 -0.25110 X09 F(31-40) 0.90316 0.21817 -0.27989 X10 F(41-) 0.79262 0.35477 -0.45389 Variance Explained by Each Factor Factor1 Factor2 Factor3 6.8279551 1.7618731 0.7544512 Final Communality Estimates: Total = 9.344279 X01 X02 X03 X04 X05 0.93786990 0.93615660 0.91021020 0.94467297 0.92966229 X06 X07 X08 X09 X10 0.94880526 0.94393897 0.89119742 0.94163724 0.96012863 Monday, November 1, 2021 09:37:03 PM 13 The FACTOR Procedure Initial Factor Method: Principal Components Scoring Coefficients Estimated by Regression Squared Multiple Correlations of the Variables with Each Factor Factor1 Factor2 Factor3 1.0000000 1.0000000 1.0000000 Standardized Scoring Coefficients Factor1 Factor2 Factor3 X01 M(-15) 0.10946 -0.33626 0.22279 X02 M(16-20) 0.12680 -0.18069 0.38691 X03 M(21-30) 0.12374 0.12531 0.50920 X04 M(31-40) 0.11455 0.27018 0.43215 X05 M(41-) 0.09978 0.38212 0.14670 X06 F(-15) 0.11811 -0.30729 -0.09636 X07 F(16-20) 0.13175 -0.19038 -0.19733 X08 F(21-30) 0.13313 -0.02434 -0.33282 X09 F(31-40) 0.13227 0.12383 -0.37099 X10 F(41-) 0.11609 0.20136 -0.60162 Monday, November 1, 2021 09:37:03 PM 14 Plot of Factor1*Factor2. Legend: A = 1 obs, B = 2 obs, etc. Factor1 | | | | 3 + | | | | | | | A 2 + |A | A A | A | A|A A | A A | A A 1 + A A A A A A | A A C A |AB A | A AA A AA | A A A | A A A BA A AA A A A 0 +-------------------A------------------A-A-----B--A-AAA---A-----A--A-- | A A A | A | A A| A A | A A A A A A A | A B A -1 + A A | A AB A A | A | A A | | AA A | A | -2 + A A | A A | | | | A | | -3 + | | | --+------------+------------+------------+------------+------------+-- -3 -2 -1 0 1 2 Factor2 Monday, November 1, 2021 09:37:03 PM 15 Plot of Factor2*Factor3. Legend: A = 1 obs, B = 2 obs, etc. Factor2 | | | | 2 + | A | A A | A | A | A | A | AA A | A | A A 1 + A A AA A| A | A A B A | A | A AA A A A| A A | A A A | A A AA A | AA AAA A | B A A 0 +----------A----B-A-----+-AB------------------------------------------ | B | BA | A A A| A A A A | A AA| A AAA | A | A -1 + A A A AA | A A A A | A AAA | A A A| A | A | -2 + AA | | | | | | | | | A -3 + | | | --+----------+----------+----------+----------+----------+----------+- -2 -1 0 1 2 3 4 Factor3 - 解釈方法 : 因子の特徴付け : 因子負荷量の大小から。
- 固有値(Eigenvalue)
- 因子毎の分散(Variance explained by each factor) : 因子毎の説明量。
- 共通性(Final Communality Estimates, Σaj^2) : 変数毎の説明割合。
- 寄与率(Proportion) : 各因子の説明力の大きさ
- 累積寄与率(Cumulative)
- 3因子まとめての説明力の大きさ : 93.4%
- 因子負荷量(標準化スコア係数, Standardized Scoring Coefficients) :
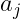: ラインマーカーの利用が効果的
- 第1因子 : 全体的な嗜好
- 第2因子 : 年齢効果 (+ 年輩、- 若年)
- 第3因子 : 性別効果 (+ 男性、- 女性)
- 各個体の因子得点(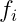)の散布図 :
- 各個体の具体的な位置を把握
- 第2因子と第3因子の関係が面白そう
- 回転の不定性から。
- 回転させた方が解釈がし易いことも多いから。
- 代表的な直交回転のVarimaxを適用してみる
- SASプログラム : FA0613.sas
- 出力結果 : FA0613-Results.txt,
FA0613_Output.pdf,
FA0613_Output.html
Monday, November 1, 2021 09:38:49 PM 51 The FACTOR Procedure Input Data Type Raw Data Number of Records Read 100 Number of Records Used 100 N for Significance Tests 100 Monday, November 1, 2021 09:38:49 PM 52 The FACTOR Procedure Initial Factor Method: Principal Components Prior Communality Estimates: ONE Eigenvalues of the Correlation Matrix: Total = 10 Average = 1 Eigenvalue Difference Proportion Cumulative 1 6.82795512 5.06608201 0.6828 0.6828 2 1.76187311 1.00742187 0.1762 0.8590 3 0.75445124 0.49207487 0.0754 0.9344 4 0.26237637 0.14082435 0.0262 0.9607 5 0.12155202 0.02358655 0.0122 0.9728 6 0.09796547 0.02586580 0.0098 0.9826 7 0.07209967 0.02801926 0.0072 0.9898 8 0.04408041 0.00832792 0.0044 0.9942 9 0.03575249 0.01385842 0.0036 0.9978 10 0.02189408 0.0022 1.0000 3 factors will be retained by the NFACTOR criterion. Monday, November 1, 2021 09:38:49 PM 53 The FACTOR Procedure Initial Factor Method: Principal Components Factor Pattern Factor1 Factor2 Factor3 X01 M(-15) 0.74741 -0.59244 0.16808 X02 M(16-20) 0.86579 -0.31836 0.29190 X03 M(21-30) 0.84491 0.22079 0.38417 X04 M(31-40) 0.78216 0.47602 0.32604 X05 M(41-) 0.68129 0.67325 0.11067 X06 F(-15) 0.80647 -0.54140 -0.07270 X07 F(16-20) 0.89959 -0.33542 -0.14888 X08 F(21-30) 0.90901 -0.04289 -0.25110 X09 F(31-40) 0.90316 0.21817 -0.27989 X10 F(41-) 0.79262 0.35477 -0.45389 Variance Explained by Each Factor Factor1 Factor2 Factor3 6.8279551 1.7618731 0.7544512 Final Communality Estimates: Total = 9.344279 X01 X02 X03 X04 X05 0.93786990 0.93615660 0.91021020 0.94467297 0.92966229 X06 X07 X08 X09 X10 0.94880526 0.94393897 0.89119742 0.94163724 0.96012863 Monday, November 1, 2021 09:38:49 PM 54 The FACTOR Procedure Rotation Method: Varimax Orthogonal Transformation Matrix 1 2 3 1 0.65777 0.53529 0.52990 2 -0.73396 0.61357 0.29126 3 0.16922 0.58051 -0.79647 Rotated Factor Pattern Factor1 Factor2 Factor3 X01 M(-15) 0.95490 0.13415 0.08963 X02 M(16-20) 0.85255 0.43757 0.13357 X03 M(21-30) 0.45872 0.81076 0.20605 X04 M(31-40) 0.22027 0.90003 0.29343 X05 M(41-) -0.02727 0.84202 0.46896 X06 F(-15) 0.91555 0.05731 0.32756 X07 F(16-20) 0.81272 0.18932 0.49758 X08 F(21-30) 0.58692 0.31451 0.66919 X09 F(31-40) 0.38658 0.45484 0.76506 X10 F(41-) 0.18417 0.37847 0.88485 Variance Explained by Each Factor Factor1 Factor2 Factor3 3.9249494 2.8740019 2.5453282 Monday, November 1, 2021 09:38:49 PM 55 The FACTOR Procedure Rotation Method: Varimax Final Communality Estimates: Total = 9.344279 X01 X02 X03 X04 X05 0.93786990 0.93615660 0.91021020 0.94467297 0.92966229 X06 X07 X08 X09 X10 0.94880526 0.94393897 0.89119742 0.94163724 0.96012863 Monday, November 1, 2021 09:38:49 PM 56 The FACTOR Procedure Rotation Method: Varimax Scoring Coefficients Estimated by Regression Squared Multiple Correlations of the Variables with Each Factor Factor1 Factor2 Factor3 1.0000000 1.0000000 1.0000000 Standardized Scoring Coefficients Factor1 Factor2 Factor3 X01 M(-15) 0.35650 -0.01839 -0.21738 X02 M(16-20) 0.28150 0.18161 -0.29360 X03 M(21-30) 0.07559 0.43873 -0.30350 X04 M(31-40) -0.04982 0.47796 -0.20481 X05 M(41-) -0.19000 0.37303 0.04733 X06 F(-15) 0.28692 -0.18126 0.04983 X07 F(16-20) 0.19300 -0.16084 0.17154 X08 F(21-30) 0.04912 -0.13688 0.32854 X09 F(31-40) -0.06666 -0.06858 0.40164 X10 F(41-) -0.17324 -0.16356 0.59933 Monday, November 1, 2021 09:38:49 PM 57 Obs X01 X02 X03 X04 X05 X06 X07 X08 1 7.69 7.31 7.47 7.76 7.87 7.51 7.24 7.70 2 6.59 5.56 6.21 6.04 5.81 6.64 6.11 6.53 3 4.55 4.18 4.36 4.25 4.53 4.60 3.66 4.04 4 6.78 6.11 6.30 5.98 5.56 6.37 6.29 5.43 5 6.47 6.24 6.02 5.42 5.88 6.00 5.60 4.60 6 6.96 6.81 6.91 6.48 6.23 7.09 7.27 7.13 7 6.57 5.70 5.89 5.16 5.30 6.07 5.56 4.50 8 7.32 6.95 6.02 4.98 4.88 6.82 6.40 5.53 9 6.51 6.15 5.51 4.68 4.16 5.17 4.81 4.70 10 6.86 6.05 5.85 6.14 6.75 6.71 5.39 5.42 11 7.04 6.03 6.53 6.02 6.68 6.78 5.91 6.26 12 6.59 6.30 6.29 5.94 6.10 5.93 5.52 5.35 13 5.93 4.76 5.09 5.51 5.79 5.49 4.97 4.69 14 7.00 6.31 6.82 6.26 5.26 6.69 6.27 5.94 15 6.63 5.47 5.54 4.88 4.70 5.89 4.64 4.43 16 6.56 6.57 5.74 4.76 4.39 6.56 6.29 5.61 Obs X09 X10 Factor1 Factor2 Factor3 1 7.91 7.95 0.66956 1.82121 1.58069 2 6.44 6.64 0.16626 -0.19916 1.19252 3 3.68 4.43 -1.03468 -1.43973 -0.47173 4 5.32 5.28 0.63900 0.22553 -0.50004 5 5.40 5.95 0.18242 0.09152 -0.20811 6 6.86 7.36 0.74034 0.36710 1.34854 7 4.92 5.33 0.32215 -0.32438 -0.54816 8 5.61 5.33 1.29334 -0.70969 -0.33933 9 4.86 3.82 0.58581 -0.75180 -1.38820 10 6.03 6.59 0.02089 0.39898 0.55070 11 5.76 5.95 0.40396 0.58950 0.17643 12 5.45 5.85 0.19873 0.54822 -0.27773 13 5.30 5.61 -0.59976 -0.44330 0.31921 14 5.78 5.26 0.91645 0.42072 -0.53512 15 4.00 3.98 0.46299 -0.53468 -1.57421 16 5.22 4.72 1.10983 -1.07931 -0.45219 ≪中略≫ Monday, November 1, 2021 09:38:49 PM 64 Plot of Factor1*Factor2. Legend: A = 1 obs, B = 2 obs, etc. 2 + | A | A | | | | A A A | | A A | A A | A |A A | A A | A A 1 + | A | A B | B A | A A AA A A A A Factor1 | A A A A A A | A A | A A A A | A | A A | A |A A A 0 +--------------------------------A-+-A-A------------------------------ | A A A | AA | A AA | A A A | A A| A A | AA | | | | A A|A BA A -1 + A AA A | A | A A | A | A A A | A A | AA A | A A | | A | | | A A | -2 + A| A --+----------+----------+----------+----------+----------+----------+- -3 -2 -1 0 1 2 3 Factor2 Monday, November 1, 2021 09:38:49 PM 65 Plot of Factor2*Factor3. Legend: A = 1 obs, B = 2 obs, etc. Factor2 | | | | 3 + | | A | | A | | | 2 + A | | | A A | A A | A A | A A | A A 1 + | AAA A A A A | | A A A | A A A A A AA |AAA A | B A AA A| A AA A A A 0 +-------------------------------------A-----A-+--AA---AAAA------------ | AA |AB A AB A | A A AA| AAA A A A | A A A A | A A -1 + A A| A A | A A A A | A A A | A A | A AA | A A A | -2 + A | | | | | | | -3 + | | | --+----------+----------+----------+----------+----------+----------+- -4 -3 -2 -1 0 1 2 Factor3 Monday, November 1, 2021 09:38:49 PM 66 Plot of Factor3*Factor1. Legend: A = 1 obs, B = 2 obs, etc. Factor3 | | | | 2 + | | A | A | A A |A AA | A | A AA 1 + A A A A | AA | A AAA AA CB | A A | A A A AA A A | A A A A A A A | AB AA B A AA 0 +---------------------A------------------+--A---------------B--------- | A | AA A AA A A | A A A A| A A A A A A | A A | A AAA A -1 + A A A| AA | A A | | A A |A A A A | | -2 + | | A | | | A | A | -3 + | | | | A | | | -4 + | | | --+------------+------------+------------+------------+------------+-- -3 -2 -1 0 1 2 Factor1 - 解釈方法 : 因子の特徴付け : 因子負荷量の大小から。
- (回転行列, Orthogonal Transformation Matrix)
- 因子毎の分散(Variance explained by each factor) : 因子毎の説明量。
- 共通性(Final Communality Estimates, Σaj^2) : 変数毎の説明割合。
- 寄与率(Proportion) : 各因子の説明力の大きさ
- 累積寄与率(Cumulative) :
- 3因子まとめての説明力の大きさ : 93.4%
- 因子負荷量(標準化スコア係数, Standardized Scoring Coefficients) :
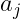
- 第1因子 : 若年層の嗜好 (+ 若年、- 年輩)
- 第2因子 : 成人男性の嗜好 (+ 成年男子)
- 第3因子 : 成人女性の嗜好 (+ 成年女子)
- 各個体の因子得点(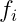)の散布図 :
参考までに食品番号でプロットしてみると。
- 各個体の具体的な位置を把握
- 各因子間の関係が面白い。
- 回転前と回転後でどのように解釈が変化したか?
- 代表的な回転法 :
- バリマックス法(rotate=varimax) : 直交回転 : 因子軸間は直交(因子軸同士は独立(無相関))
- プロマックス法(rotate=promax) : 斜交回転 : 因子軸間に相関性
- p次元を何次元に縮約するかの因子数は利用者側から与える必要がある。 ===> 上記3因子で解釈に無理はないか?
- 近傍の因子数(2とか4とか)で試してみるのも一案である。
- 回転させないときと、回転させたときでどちらが解釈が容易か?
- 因子数を指定して分析を進める必要があるため、 前処理や確定した因子数に基づく分析等、 行きつ戻りつの試行錯誤が必要な手法である。
- データのバックグラウンドを把握していると、因子の解釈を行い易い。
- 明確に決まっているわけではない : 主成分分析と同様
- 結果の解釈の都合上、多少増減させることもある : 試行錯誤
- 累積寄与率がある程度(例えば80%以上)以上大きくなること
- 固有値のギャップがある程度以上大きいこと
- 固有値が 1以上
- ...
- 目的: いくつか(p個)の変量の情報を、損失をできるだけ少なくして、 少数変量(m個、m＜p)の総合的指標(主成分)で代表させたい。
- 考え方
- 主成分分析 : 分散最大
- 因子分析 : モデルの導入、回転性、一意性に疑問(特に斜交回転)
- 対象データ
- サンプルサイズのある程度大きいデータが対象となる
- 変量数もある程度大きいデータが対象となる
- 当然ながらサンプルサイズの方が変量数よりも大きいこと : 多変量解析全般
- 対象データを熟知している方が解釈しやすい(熟知の必要性)
- 因子の特徴付けはデータのバックグラウンドに深く関係
- 経験を積むとより納得する説明ができる
- 潜在的な構造が仮定できるか? モデルが適用可能な問題か吟味する必要性。
- 軸数、主成分数、因子数を変えて解釈を行ってみる。行きつ戻りつして試行錯誤してみる。
-
[ノウハウ] ラインマーカーで絶対値の大きい変量にマークを付ける
- いろいろなデータで経験を積んでみる。
- どっちを使う? : やってみる。解釈してみる。今までの事例と比較してみる。
- ...
- データによっては解釈が困難なことも有り得る。 また、自分の思い付かない結果を含んでいることもある。
[例] 関西学院大学: 中央値補正法とは...
.、
科目別平均点の中央値補正前後比較
.
[例] 関西大学: 各学部での合否判定の方法