DS2407_8
Hayashi Atsuhiro
2024/11/14
8. 因子分析: モデル(概要)
いくつか(p個)の変量の値を情報の損失をできるだけ少なくして、少数変量(m個、m＜p)の総合的指標(主成分)で代表させる方法として、先週は主成分分析(Principal Component Analysis, PCA)を学んだ。この手法は データの散らばり方(分散)を捉えてデータ特性を把握する手法であった。 一方、因子分析(Factor Analysis, FA)は、変数間に(潜在的な)構造を持ち込んで 関係を探る手法である(少し理解しにくいかもしれないが)。 この手法は心理学の分野で広く利用されている。
-
定式化
-
例えば、i番目の学生の3科目の試験成績
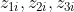が得られていたとする(i=1,2,…,n)。
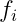をi番目の学生の特徴を表す要素、
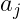をj番目の科目の特徴を表す要素とし、
それらが以下のような積の形で表現できたとしたら、学生個人と科目の特性が分離できることになる。
-
-
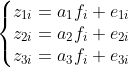
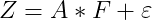
ここで、
-
測定対象
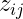: 成績、測定値、…。
-
共通因子(潜在変量) :
:
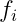因子得点(測定できない潜在変量)、個体の特徴付け、i=1,2,3,…,n.
-
因子負荷量(潜在変量) :
:
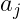因子の特徴付け、j=1,2,3,…,p.
-
独自因子 :
:
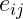変動、誤差
-
測定対象
-
いくつかの仮定 :
,
,
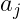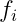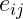の下で、これらを満たす
,
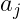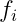を求める。
-
回転の不定性:
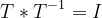となる回転行列Tを用いると、
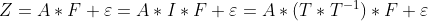
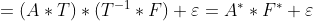
となり、AとFの対は無限組存在する。一意には決まらない。 何らかの基準を条件に確定させる。
-
-
p次元を何次元に縮約するかの軸数(因子数)も利用者側から与える必要がある。
- 因子の解釈
- 因子軸の回転 : 直交回転、斜交回転
- 因子数を指定して分析を進める必要があるため、 前処理や確定した因子数に基づく分析等、 行きつ戻りつの試行錯誤が必要な手法である。
9. [例題FA] 食品の嗜好性を探ってみよう (変量数の少ないデータに当てはめてもあまり有効性を感じられないため)
-
まずは因子数を決めよう
- 固有値(Eigenvalue) : 相関行列の固有値の振る舞いから因子数(軸数、m)を決める。
- 固有値の割合、累積割合
- 固有値間のギャップ(減少具合) 等 ===> Scree Plotが便利
# データの読み込み Food<-read.csv("food.csv", skip=17, header=TRUE) dim(Food)## [1] 100 10# colnames(Food) Food[1:5,]## M1 M2 M3 M4 M5 F1 F2 F3 F4 F5 ## 1 7.69 7.31 7.47 7.76 7.87 7.51 7.24 7.70 7.91 7.95 ## 2 6.59 5.56 6.21 6.04 5.81 6.64 6.11 6.53 6.44 6.64 ## 3 4.55 4.18 4.36 4.25 4.53 4.60 3.66 4.04 3.68 4.43 ## 4 6.78 6.11 6.30 5.98 5.56 6.37 6.29 5.43 5.32 5.28 ## 5 6.47 6.24 6.02 5.42 5.88 6.00 5.60 4.60 5.40 5.95Food_cor<-cor(Food) # 相関行列 Food_cor## M1 M2 M3 M4 M5 F1 F2 ## M1 1.0000000 0.8707502 0.5158024 0.3701171 0.1722555 0.9383574 0.8106677 ## M2 0.8707502 1.0000000 0.7588002 0.6042866 0.4021423 0.8206969 0.8380528 ## M3 0.5158024 0.7588002 1.0000000 0.8524283 0.7261755 0.5164491 0.6583837 ## M4 0.3701171 0.6042866 0.8524283 1.0000000 0.8742306 0.3580258 0.4875341 ## M5 0.1722555 0.4021423 0.7261755 0.8742306 1.0000000 0.2077093 0.3543237 ## F1 0.9383574 0.8206969 0.5164491 0.3580258 0.2077093 1.0000000 0.8887956 ## F2 0.8106677 0.8380528 0.6583837 0.4875341 0.3543237 0.8887956 1.0000000 ## F3 0.6160570 0.7095440 0.6989555 0.6198739 0.5234535 0.7464624 0.8949360 ## F4 0.5003457 0.6469773 0.7013245 0.7206826 0.7100951 0.6214719 0.7678802 ## F5 0.3298161 0.4569242 0.5584082 0.6321387 0.7479457 0.4931943 0.6415215 ## F3 F4 F5 ## M1 0.6160570 0.5003457 0.3298161 ## M2 0.7095440 0.6469773 0.4569242 ## M3 0.6989555 0.7013245 0.5584082 ## M4 0.6198739 0.7206826 0.6321387 ## M5 0.5234535 0.7100951 0.7479457 ## F1 0.7464624 0.6214719 0.4931943 ## F2 0.8949360 0.7678802 0.6415215 ## F3 1.0000000 0.8528403 0.7741073 ## F4 0.8528403 1.0000000 0.9111652 ## F5 0.7741073 0.9111652 1.0000000Food_eigen<-eigen(Food_cor)$values # 相関行列の固有値を求める Food_eigen # 個々の固有値を表示させる## [1] 6.82795512 1.76187311 0.75445124 0.26237637 0.12155202 0.09796547 ## [7] 0.07209967 0.04408041 0.03575249 0.02189408Food_eigen_Prop<-Food_eigen/sum(Food_eigen) Food_eigen_Prop # 個々の固有値の割合## [1] 0.682795512 0.176187311 0.075445124 0.026237637 0.012155202 0.009796547 ## [7] 0.007209967 0.004408041 0.003575249 0.002189408cumsum(Food_eigen_Prop) # 固有値の累積割合## [1] 0.6827955 0.8589828 0.9344279 0.9606656 0.9728208 0.9826173 0.9898273 ## [8] 0.9942353 0.9978106 1.0000000Scree Plot: 各軸の寄与の大きさと、減少具合が視覚的に把握できる。
# 固有値のScree Plot(現象具合が視覚的に判断できる) plot(Food_eigen, type="b", main="Scree Plot", xlab="Number", ylab="Eigen Value") abline(h=seq(0,7,1), lty=3)
- 解釈方法 : 軸の数を決めることがメイン。
- 固有値(Eigenvalue) : 相関行列の固有値
-
因子数の決定 : 解析者側の判断
- 累積寄与率(8割以上)や、固有値が1を超えているという理由からは、軸数は 2と判定されるであろう。
- 固有値の変化量(減少具合)からすると、3 でも良さそう : 3 と 4 の間が空いてるので。
- 因子数を 3 として計算してみよう
- 因子数を3に指定して解析を進める
-
関数内の引数は以下の指定を行っている。
- x=Food : データが格納された変数を指定
- factors=3 : 因子数を3に指定
- scores=“regression” : 各食品の変換後得点を計算させる
- rotation=“none” : 回転を行わない
# 因子分析(3因子、回転させず) FAresultsFood1<-factanal(x=Food, factors=3, scores="regression", rotation="none") print(FAresultsFood1, cutoff=0)## ## Call: ## factanal(x = Food, factors = 3, scores = "regression", rotation = "none") ## ## Uniquenesses: ## M1 M2 M3 M4 M5 F1 F2 F3 F4 F5 ## 0.055 0.115 0.158 0.059 0.108 0.035 0.113 0.183 0.083 0.025 ## ## Loadings: ## Factor1 Factor2 Factor3 ## M1 0.735 0.629 0.097 ## M2 0.818 0.370 0.279 ## M3 0.773 -0.109 0.482 ## M4 0.737 -0.359 0.519 ## M5 0.672 -0.589 0.305 ## F1 0.817 0.535 -0.105 ## F2 0.888 0.301 -0.091 ## F3 0.899 0.008 -0.091 ## F4 0.919 -0.249 -0.096 ## F5 0.846 -0.427 -0.276 ## ## Factor1 Factor2 Factor3 ## SS loadings 6.627 1.643 0.795 ## Proportion Var 0.663 0.164 0.080 ## Cumulative Var 0.663 0.827 0.907 ## ## Test of the hypothesis that 3 factors are sufficient. ## The chi square statistic is 158.68 on 18 degrees of freedom. ## The p-value is 1.51e-24FAresultsFood1$scores[1:8,] # 最初の8食品のスコア。$scoresに格納されている。## Factor1 Factor2 Factor3 ## [1,] 2.2521106 -0.88287388 0.5162598 ## [2,] 0.7692368 -0.22731589 -0.7536347 ## [3,] -1.5207144 0.08966597 -0.9204183 ## [4,] 0.2101671 0.59947631 0.5471236 ## [5,] 0.1764941 0.07314483 -0.3024410 ## [6,] 1.4508598 -0.32101263 -0.5919559 ## [7,] -0.1558487 0.58059684 -0.2573396 ## [8,] 0.2624901 1.30903241 -0.4316699- 解釈方法 : 因子の特徴付け : 因子負荷量
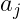の大小から。
- SS loadings: 因子寄与。因子負荷量の2乗和で、その因子が説明できる観測変数の分散の大きさ。
- Proportion Var: 因子ごとの寄与率。
-
Cumulative Var: 累積寄与率。因子寄与率の累積合計。
-
因子負荷量(Loadings,
):
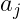ラインマーカーの利用が効果的
- 第1因子 : 全体的な嗜好
- 第2因子 : 年齢効果 (+ 若年、- 年輩)
- 第3因子 : 性別効果 (+ 男性、- 女性)
-
各個体の因子得点(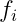)の散布図
:
- 各個体の具体的な位置を把握
- 第2因子と第3因子の関係が面白そう
# 食品番号でプロットしてみる。 plot(FAresultsFood1$scores[,2], FAresultsFood1$scores[,1], type="n") text(FAresultsFood1$scores[,2], FAresultsFood1$scores[,1]) abline(h=seq(-3,2,1), lty=3) abline(v=seq(-2,3,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
plot(FAresultsFood1$scores[,3], FAresultsFood1$scores[,2], type="n") text(FAresultsFood1$scores[,3], FAresultsFood1$scores[,2]) abline(h=seq(-2,3,1), lty=3) abline(v=seq(-2,3,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
plot(FAresultsFood1$scores[,1], FAresultsFood1$scores[,3], type="n") text(FAresultsFood1$scores[,1], FAresultsFood1$scores[,3]) abline(h=seq(-2,3,1), lty=3) abline(v=seq(-3,2,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
- 回転させてみよう : ただし、回転が必須ではない
- 回転の不定性から。
-
回転させた方が解釈がし易いことも多いから。
- 代表的な直交回転のVarimaxを適用してみる
# 回転させてみよう (3因子、varimax回転) FAresultsFood2<-factanal(x=Food, factors=3, scores="regression", rotation="varimax") print(FAresultsFood2, cutoff=0)## ## Call: ## factanal(x = Food, factors = 3, scores = "regression", rotation = "varimax") ## ## Uniquenesses: ## M1 M2 M3 M4 M5 F1 F2 F3 F4 F5 ## 0.055 0.115 0.158 0.059 0.108 0.035 0.113 0.183 0.083 0.025 ## ## Loadings: ## Factor1 Factor2 Factor3 ## M1 0.958 0.144 0.080 ## M2 0.822 0.435 0.140 ## M3 0.435 0.779 0.214 ## M4 0.223 0.899 0.289 ## M5 -0.003 0.803 0.496 ## F1 0.932 0.067 0.303 ## F2 0.800 0.211 0.450 ## F3 0.584 0.345 0.598 ## F4 0.401 0.461 0.737 ## F5 0.211 0.365 0.893 ## ## Factor1 Factor2 Factor3 ## SS loadings 3.888 2.784 2.393 ## Proportion Var 0.389 0.278 0.239 ## Cumulative Var 0.389 0.667 0.907 ## ## Test of the hypothesis that 3 factors are sufficient. ## The chi square statistic is 158.68 on 18 degrees of freedom. ## The p-value is 1.51e-24FAresultsFood2$scores[1:8,] # 最初の8食品のスコア。$scoresに格納されている。## Factor1 Factor2 Factor3 ## [1,] 0.8038420 1.8279283 1.4596263 ## [2,] 0.2952334 -0.1258134 1.0527921 ## [3,] -0.9506699 -1.4561392 -0.3790350 ## [4,] 0.6136848 0.2601240 -0.5085398 ## [5,] 0.1581896 -0.1831980 0.2634112 ## [6,] 0.6709091 0.3563798 1.4075971 ## [7,] 0.3315574 -0.5228508 -0.2104801 ## [8,] 1.1502676 -0.7789009 -0.1974930解釈方法 : 因子の特徴付け : 因子負荷量
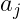の大小から。- SS loadings: 因子寄与。因子負荷量の2乗和で、その因子が説明できる観測変数の分散の大きさ。
- Proportion Var: 因子ごとの寄与率。
-
Cumulative Var: 累積寄与率。因子寄与率の累積合計。
-
因子負荷量(Loadings,
):
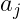ラインマーカーの利用が効果的
- 第1因子 : 若年層の嗜好 (+ 若年、- 年輩)
- 第2因子 : 成人男性の嗜好 (+ 成年男子)
- 第3因子 : 成人女性の嗜好 (+ 成年女子)
-
各個体の因子得点(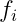)の散布図
:
- 各個体の具体的な位置を把握
- 各因子間の関係が面白い。
- 回転前と回転後でどのように解釈が変化したか?
# 食品番号でプロットしてみる。 plot(FAresultsFood2$scores[,2], FAresultsFood2$scores[,1], type="n") text(FAresultsFood2$scores[,2], FAresultsFood2$scores[,1]) abline(h=seq(-2,2,1), lty=3) abline(v=seq(-2,2,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
plot(FAresultsFood2$scores[,3], FAresultsFood2$scores[,2], type="n") text(FAresultsFood2$scores[,3], FAresultsFood2$scores[,2]) abline(h=seq(-2,2,1), lty=3) abline(v=seq(-3,1,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
plot(FAresultsFood2$scores[,1], FAresultsFood2$scores[,3], type="n") text(FAresultsFood2$scores[,1], FAresultsFood2$scores[,3]) abline(h=seq(-3,1,1), lty=3) abline(v=seq(-2,2,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)
- 代表的な回転法 :
- バリマックス法(rotation=“varimax”) : 直交回転 : 因子軸間は直交(因子軸同士は独立(無相関))
- プロマックス法(rotation=“promax”) : 斜交回転 : 因子軸間に相関性
10. 次の一手
- p次元を何次元に縮約するかの因子数は利用者側から与える必要がある。 ===> 上記3因子で解釈に無理はないか?
- 近傍の因子数(2とか4とか)で試してみるのも一案である。
-
回転させないときと、回転させたときでどちらが解釈が容易か?
- 因子数を指定して分析を進める必要があるため、 前処理や確定した因子数に基づく分析等、 行きつ戻りつの試行錯誤が必要な手法である。
- データのバックグラウンドを把握していると、因子の解釈を行い易い。
11. 因子数の決定基準
- 明確に決まっているわけではない : 主成分分析と同様
-
結果の解釈の都合上、多少増減させることもある : 試行錯誤
- 累積寄与率がある程度(例えば80%以上)以上大きくなること
- 固有値のギャップがある程度以上大きいこと
- 固有値が 1以上
- …
12. 主成分分析(PCA)と因子分析(FA): 目的は同じでもアイディアが異なる手法
-
目的: いくつか(p個)の変量の情報を、損失をできるだけ少なくして、
少数変量(m個、m＜p)の総合的指標(主成分)で代表させたい。
-
考え方
- 主成分分析 : 分散最大
- 因子分析 : モデルの導入、回転性、一意性に疑問(特に斜交回転)
-
対象データ
- サンプルサイズのある程度大きいデータが対象となる
- 変量数もある程度大きいデータが対象となる
- 当然ながらサンプルサイズの方が変量数よりも大きいこと : 多変量解析全般
- 対象データやその採取背景を熟知している方が解釈しやすい(熟知の必要性)
- 因子の特徴付けはデータのバックグラウンドに深く関係
- 経験を積むとより納得する説明ができる
-
潜在的な構造が仮定できるか? モデルが適用可能な問題か吟味する必要性。
-
軸数、主成分数、因子数を変えて解釈を行ってみる。行きつ戻りつして試行錯誤してみる。
-
[ノウハウ]
ラインマーカーで絶対値の大きい変量にマークを付ける
- いろいろなデータで経験を積んでみる。
- どっちを使う? : やってみる。解釈してみる。今までの事例と比較してみる。
-
…
- データによっては解釈が困難なことも有り得る。 また、自分の思い付かない結果を含んでいることもある。
13. “データサイエンス”に求められるもの
私の担当部分を終えるにあたって、これまでの経験から データサイエンスに付いての若干の私見を述べる。-
ビッグデータ: 明確な定義はない
- 3V: Volume(容量), Velocity(更新頻度), Variety(多様性)
-
AI ブーム: 過去の蓄積から似たデータを取り出し、提示する。
-
「押し寄せてくるデータ」への対処
- データストレージの発達
- センサーの充実、普及 ===> 大量データの生成時代
-
【これまで】 能動的なデータ採取 ===> 【これから】 受動的なデータ採取
-
初等中等教育にも「統計教育」が導入。大学入試には
H27年度から。R7からは新教育課程対応入試。
- 思考力、判断力、表現力、読解力
- 「統計的なものの見方や考え方」を身に付ける
- 知識暗記型の教育からの脱皮 ===> データに基づいた問題解決力の育成
- 社会を生き抜いていくための有用なスキル
-
ビッグデータ時代のデータサイエンス
- 分析結果の質 <=== データの質に依存
-
「データの取り扱い」を中心に据えた分析姿勢
- 「膨大なデータを前にして本質を見抜く力」
- 重要: データ＋教育＋現場主義
14. 最終レポート(再掲)
【最終レポート(後期前半)】
以下の事項について、WordファイルもしくはPDFファイルでレポートを作成し、Moodleから提出下さい。なお、提出フォームは11月14日(木)
昼から利用可能となります。
1.【必須項目】
かねてからお伝えしていたように、各自が興味を持って収集したデータに対して統計手法を適用し、何らかの知見を引き出して報告してください。統計手法として、本講義で紹介した統計手法には限定しません。また、対象とするデータは1つ以上いくつでもかまいません。
-
◎記載内容: 以下に挙げるような項目を含めて作成すること。
- 所属学部名、学籍番号、氏名
- データ内容の説明
- どのような点に興味を持ったか
- 自分の解析目的
- 何を知りたいためにどのような手法を使ったのか
- 得られた知見と考察
- その他、気付いたこと
2.【必須項目】
本講義の初回に「統計」に抱くイメージを聞かせてもらった。その後、本講義を受講することによってそのイメージは変化したか。
講義を聞き終えた現状でどのように感じているか、また今後ご自身として統計に対してどのように取り組みたい/取り組みたくないかを説明せよ。
3.【任意項目】
講義方法、講義の進め方等の感想(コメントがあれば嬉しいな)
講義内容の感想だけでなく、講義方法等に付いて気になった点や感想、改善希望点をお聞かせください。
【注意】単位取得を考えている者は期日までに提出すること。
15. 後期前半を終えるにあたって
この講義を通して、「統計」や「データ解析」と言う言葉に多少なりとも親しみを持っていただけただろうか? RやRStudioの使い方に始まり、多変量解析と呼ばれる統計手法を幾つか紹介したが、数式自身よりもその手法の考え方や利用目的に重点をおいて説明したつもりである。 今回の講義を通してRのプログラムも自分で作成・修正ができるようになっていることを期待する。Rには多くの統計手法が準備されているので、今後は必要に応じてそれらを逐次追加しながら獲得していけばより広範な統計手法を利用することができるであろう。加えてサポートメンバーに依る強力なライブラリー群も提供されているので、将来的にはそれらを利用して分析を進めることを考えても良いのかもしれない。
今後、新聞や雑誌と言った生活では勿論のこと、研究やいろいろな場面で、種々の数値列に出会うことになると思うが、提示された数値にはどの様な意味(と意図)があり、 どう理解して、個々人としてどうアクションを起すかの、一つの判断手段として活用してもらえれば幸いである。
なお、今後、もし統計に関して何か疑問に出会い、私に相談してみたいと思われたら、遠慮無くご連絡下さい。
皆さんの期待に応えられたか心許無い部分もありますが、7回、お付き合いくださり、どうもありがとうございました。お疲れさまでした。
82. 参考
このページで取り扱ったプログラムだけを抜き出して以下に列挙しておく。
# ディレクトリの移動。必須ではない。個々人の設定に応じて。
setwd("D:/home_sub3/R_Dir") # ホームディレクトリに移動(Set Working Directory)
getwd() # 現在のディレクトリ位置を表示
list.files() # ファイル・ディレクトリ一覧を表示
setwd("KougiDS24") # ディレクトリを移動
list.files() # ファイル・ディレクトリ一覧を表示
# データの読み込み
Food<-read.csv("food.csv", skip=17, header=TRUE)
dim(Food)
# colnames(Food)
Food[1:5,]
Food_cor<-cor(Food) # 相関行列
Food_cor
Food_eigen<-eigen(Food_cor)$values # 相関行列の固有値を求める
Food_eigen # 個々の固有値を表示させる
Food_eigen_Prop<-Food_eigen/sum(Food_eigen)
Food_eigen_Prop # 個々の固有値の割合
cumsum(Food_eigen_Prop) # 固有値の累積割合
# 固有値のScree Plot(現象具合が視覚的に判断できる)
plot(Food_eigen, type="b", main="Scree Plot", xlab="Number", ylab="Eigen Value")
abline(h=seq(0,7,1), lty=3)
# 因子分析(3因子、回転させず)
FAresultsFood1<-factanal(x=Food, factors=3, scores="regression", rotation="none")
print(FAresultsFood1, cutoff=0)
FAresultsFood1$scores[1:8,] # 最初の8食品のスコア。$scoresに格納されている。
# 食品番号でプロットしてみる。
plot(FAresultsFood1$scores[,2], FAresultsFood1$scores[,1], type="n")
text(FAresultsFood1$scores[,2], FAresultsFood1$scores[,1])
abline(h=seq(-3,2,1), lty=3)
abline(v=seq(-2,3,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(FAresultsFood1$scores[,3], FAresultsFood1$scores[,2], type="n")
text(FAresultsFood1$scores[,3], FAresultsFood1$scores[,2])
abline(h=seq(-2,3,1), lty=3)
abline(v=seq(-2,3,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(FAresultsFood1$scores[,1], FAresultsFood1$scores[,3], type="n")
text(FAresultsFood1$scores[,1], FAresultsFood1$scores[,3])
abline(h=seq(-2,3,1), lty=3)
abline(v=seq(-3,2,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
# 回転させてみよう (3因子、varimax回転)
FAresultsFood2<-factanal(x=Food, factors=3, scores="regression", rotation="varimax")
print(FAresultsFood2, cutoff=0)
FAresultsFood2$scores[1:8,] # 最初の8食品のスコア。$scoresに格納されている。
# 食品番号でプロットしてみる。
plot(FAresultsFood2$scores[,2], FAresultsFood2$scores[,1], type="n")
text(FAresultsFood2$scores[,2], FAresultsFood2$scores[,1])
abline(h=seq(-2,2,1), lty=3)
abline(v=seq(-2,2,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(FAresultsFood2$scores[,3], FAresultsFood2$scores[,2], type="n")
text(FAresultsFood2$scores[,3], FAresultsFood2$scores[,2])
abline(h=seq(-2,2,1), lty=3)
abline(v=seq(-3,1,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(FAresultsFood2$scores[,1], FAresultsFood2$scores[,3], type="n")
text(FAresultsFood2$scores[,1], FAresultsFood2$scores[,3])
abline(h=seq(-3,1,1), lty=3)
abline(v=seq(-2,2,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)