DS2402_2
Hayashi Atsuhiro
2024/10/10
2. 【再掲】画面構成とそれぞれのペインの役割
-
RStudioの起動
- スタートメニューから「RStudio」→「RStudio」
- または、デスクトップに表示されているrstudioのアイコン(右図)をクリックしてRStudioを起動する
-
RはRStudio内から操作されるので陽に意識する必要はない
-
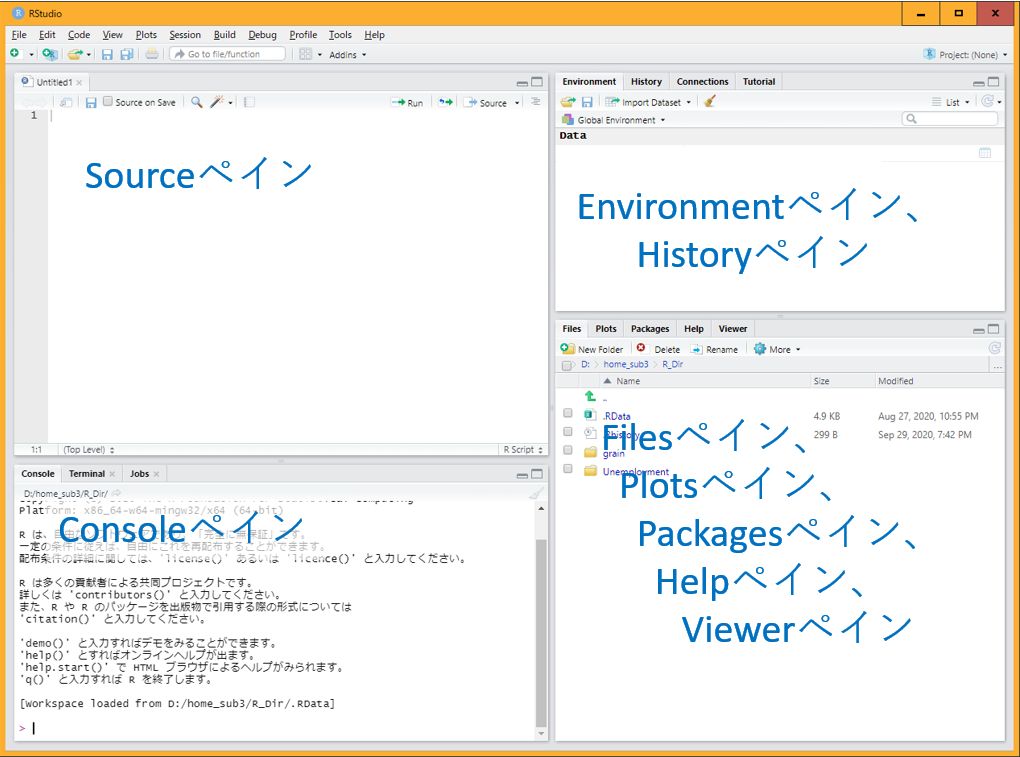
画面の説明: 4つの画面がありそれぞれに役割あり
- 左上: Sourceペイン <=== プログラムを入力する
- 左下: Consoleペイン <=== 計算結果が表示される
- 右上: Environmentペイン、Historyペイン
- 右下: Filesペイン、Plotsペイン、Packagesペイン、 Helpペイン、Viewerペイン
- [補足1] 初回起動時には「Enable Automated Crash Reporting」というアラートウインドウが表示されるが、バグレポートに協力するか否かを問うているので、ご自身で判断いただいて先に進んでください(Yes/No)。
- [補足2] ConsoleペインにはインストールしたRのバージョンが表示されているはずである。今回の例で言えば「R version 4.3.1 (2024-06-16 ucrt)」と表示されているのではないか。
- [補足3] ペインが3つしか表示されておらずSourceペインが1行しか表示されていなかったら、Consoleペインの右上部(バー右端)をダブルクリックする。
- 手始めに簡単な操作を行ってみる
-
Sourceペイン(左上の領域)で
- 「5+3」と入力後、「Ctrl+Enter」(Ctrlキーを押しながら、Enterキーを押す)を行うと、Consoleペインに「8」と計算結果が出力される。
- 「5^3」と入力後、「Ctrl+Enter」を行うと、Consoleペインに「125」と計算結果が出力される。
- 演算記号: 四則演算(+、ー、*、/)、べき乗: ^、剰余: %%、平方根: sqrt()
5+3 # 加算## [1] 85^3 # べき乗## [1] 1255%%3 # 剰余## [1] 2sqrt(5) # 平方根## [1] 2.236068【補足】以後、資料中の、灰色の囲みエリアは、Sourceペインでの利用者の入力画面を示し、白い囲みエリアはConsoleペインのシステムからの計算結果画面を示す。 また「#」(半角)マークより右側は利用者への説明のためのコメントであり、計算には影響しない。
[演習2-1] 上記演算子を用いて各自で任意の計算を行ってみよ。
- 電卓のような使い方。より複雑な利用方法は後述。
任意の「式を入力」後、「Ctrl+Enter」で実行する。
∞. 【先週はこのあたりまで説明した】
3. Rでプログラムが書けるようになろう
データを格納するために、変数やベクトル、行列の取り扱いを理解しよう。
3.1. 変数とベクトルを理解する
値を保持させるものとして、英数字で変数を定義できる。 左矢印(に見えるかな?)で値を代入している(定義している)ことを示している。 その際、英字の大文字と小文字は別のものとして取り扱われることに注意せよ。
[操作] Sourceペイン(左上)に1行入力するごとに、「Ctrl+Enter」で実行する。 計算結果はConsoleペイン(左下)に表示される。以下では、薄い灰色部分が Sourceペインの入力を示している。このテキストからコピーペーストすれば手入力の手間を省くことができる。また、複数行を選択(ハイライト)後、 「Ctrl+Enter」をすると、複数行を一気に実行することができる。
なお、新たに定義された変数は、Environmentペイン(右上)に表示される。 また、シャープ記号(#)の後ろは「コメント」であり、Rの実行には無関係である。読者への説明用に記入してある。
5人の身長の平均を求めてみよう
身長: 156, 162, 166, 174, 178
皆さんのアンケートの中から、任意の5人を抽出して、 この5人のデータに対する処理方法を紹介する。
Xvec<-c(156,162,166,174,178) # 要素数5のベクトルの定義(方法2)
Xvec # 定義したベクトルを表示させてみる## [1] 156 162 166 174 178mean(Xvec) # ベクトルの要素の平均値を求める## [1] 167.2[演習3.1-1] 上記5人のそれぞれの体重は以下であった。平均値を求めよ。
体重: 50, 65, 57, 82, 67
Yvec<-c(50,65,57,82,67) # 方法2
Yvec## [1] 50 65 57 82 67mean(Yvec)## [1] 64.2【要点】
- ベクトルの生成方法に慣れよ。c()関数のcはcombinationの頭文字の意味。
- 1行ずつ実行するには式を入力後、「Ctrl+Enter」を押す。
- まとめて実行するには、式を複数行を選択後、「Ctrl+Enter」を押す。
- 「#」以降は注釈(コメント)で実行には影響を与えない。
- 特定の要素の値を見るには角括弧で要素番号を指定する。
Xvec[1] # 1番目の要素の値は 156 =1人目の身長## [1] 156Yvec[4] # 4番目の要素の値は 82 =4人目の体重## [1] 823.2. 行列への拡張
統計では、縦方向にサンプル(1人目、2人目、…)を、 横方向に変量(身長、体重等)を2次元的に配置して分析に供することが一般的である。
ベクトルを横方向に連結して行列を作る。ここでは取り上げないが、 新たなサンプルが採取できたような場合(サンプルの追加)は、縦方向に連結する(行結合する)ことになる。
- cbind()の名称はcolumn bind (列結合とでも訳すのか)
- rbind()の名称はrow bind (行結合とでも訳すのか)
XYmatrix<-cbind(Xvec,Yvec)
XYmatrix## Xvec Yvec
## [1,] 156 50
## [2,] 162 65
## [3,] 166 57
## [4,] 174 82
## [5,] 178 67特定の要素の値を参照するには角括弧で要素番号を指定する。
XYmatrix[1,1] # (1,1)の要素の値は179 =1人目の身長## Xvec
## 156XYmatrix[4,2] # (4,2)の要素の値は61 =4人目の体重## Yvec
## 82XYmatrix[,1] # 2次元目が1の要素を順に表示(=身長を全部表示)## [1] 156 162 166 174 178XYmatrix[3,] # 1次元目が3の要素を順に表示(3人目の要素を全部(身長と体重)表示)## Xvec Yvec
## 166 57[演習3.2-1] 行列に対してmean()を適用したらどうなるか、各自でやってみよ。得られた値は何を示しているのか?
mean(XYmatrix)## [1] 115.7[演習3.2-2] では、身長や体重のデータが格納されて行列に対して、身長の平均値や体重の平均値を求めるにはどのように指定すれば良いだろうか? 各自考えて試してみよ。
mean(XYmatrix[,1]) # 身長の平均値を求める
## [1] 167.2
mean(XYmatrix[,2]) # 体重の平均値を求める
## [1] 64.2[演習3.2-3: 発展] 身長の平均の求め方は判った。では、身長の分散を計算するにはどのように式を書けば良いであろうか。
# 方法1
sum((XYmatrix[,1]-mean(XYmatrix[,1]))^2)/(length(XYmatrix[,1])-1) # 一発で書くと
# 方法2: 方法1の各項を変数に代入して逐次的に値を確認してみる
XHensa<-XYmatrix[,1]-mean(XYmatrix[,1]) # 平均との偏差
XHensaSq<-XHensa^2 # 偏差の2乗
XHensaSqSum<-sum(XHensaSq) # 偏差の2乗和
Xlen<-length(XYmatrix[,1]) # データの個数
XVar<-XHensaSqSum/(Xlen-1) # 分散
XHensa # 平均との偏差
XHensaSq # 偏差の2乗
XHensaSqSum # 偏差の2乗和
Xlen # データの個数
XVar # 分散
# 方法3
var(XYmatrix[,1]) # 身長の分散を求める
# 方法1
## [1] 79.2# 方法2
## [1] -11.2 -5.2 -1.2 6.8 10.8## [1] 125.44 27.04 1.44 46.24 116.64## [1] 316.8## [1] 5## [1] 79.2# 方法3
## [1] 79.23.3. 便利な関数: seq(), rep()
今後利用することになる関数のいち部を紹介しておく。 単体では「ありがたみ」が判らないかもしれないが、 グラフの軸ラベル等に使ったりする。
- seq()の名称はsequential (一連のとでも訳すのか)
- rep()の名称はrepetition (繰り返しとでも訳すのか)
seq(1:10) # 1から10まで10個の要素のベクトルを生成(1つずつ順に))## [1] 1 2 3 4 5 6 7 8 9 10seq(10,100,10) # 10から100まで10飛ばしで10個の要素のベクトルを生成## [1] 10 20 30 40 50 60 70 80 90 100rep(3,8) # 3を8回繰り返す## [1] 3 3 3 3 3 3 3 33:7 # 3から7までを順に表示## [1] 3 4 5 6 7rep(3:7,3) # {3,4,5,6,7}のベクトルを3回繰り返す## [1] 3 4 5 6 7 3 4 5 6 7 3 4 5 6 74. ここまでのまとめ
【思い】Rにおけるベクトルと行列の取り扱いや概念を習得してほしい。
【紹介した関数】代入(<-), +, -, *, /, ^, %%, sqrt(), mean(), var(),
c(), cbind(), rbind(), seq(), rep()
【紹介したコマンド】list.files(), getwd(), setwd()
【参考】各ペインに何が表示されているかを見てみよう。
- Sourceペイン(左上): 命令、プログラム
- Consoleペイン(左下): 計算結果
- Environemntペイン(右上): 各変数の値
- Historyペイン(右上): これまで入力してきた命令一覧
82. 参考
このページで取り扱ったプログラムだけを抜き出して以下に列挙しておく。
## 2. 【再掲】画面構成とそれぞれのペインの役割
5+3 # 加算
5^3 # べき乗
5%%3 # 剰余
sqrt(5) # 平方根
## 3. Rでプログラムが書けるようになろう
## 3.1. 変数とベクトルを理解する
Xvec<-c(156,162,166,174,178) # 要素数5のベクトルの定義(方法2)
Xvec # 定義したベクトルを表示させてみる
mean(Xvec) # ベクトルの要素の平均値を求める
# [演習3.1-1]
Yvec<-c(50,65,57,82,67) # 方法2
Yvec
mean(Yvec)
Xvec[1] # 1番目の要素の値は 156 =1人目の身長
Yvec[4] # 4番目の要素の値は 82 =4人目の体重
## 3.2. 行列への拡張
XYmatrix<-cbind(Xvec,Yvec)
XYmatrix
XYmatrix[1,1] # (1,1)の要素の値は156 =1人目の身長
XYmatrix[4,2] # (4,2)の要素の値は82 =4人目の体重
XYmatrix[,1] # 2次元目が1の要素を順に表示(=身長を全部表示)
XYmatrix[3,] # 1次元目が3の要素を順に表示(3人目の要素を全部(身長と体重)表示)
# [演習3.2-1]
mean(XYmatrix)
# [演習3.2-2]
mean(XYmatrix[,1]) # 身長の平均値を求める
mean(XYmatrix[,2]) # 体重の平均値を求める
# [演習3.2-3: 発展]
# 方法1
sum((XYmatrix[,1]-mean(XYmatrix[,1]))^2)/(length(XYmatrix[,1])-1) # 一発で書くと
# 方法2: 方法1の各項を変数に代入して逐次的に値を確認してみる
XHensa<-XYmatrix[,1]-mean(XYmatrix[,1]) # 平均との偏差
XHensaSq<-XHensa^2 # 偏差の2乗
XHensaSqSum<-sum(XHensaSq) # 偏差の2乗和
Xlen<-length(XYmatrix[,1]) # データの個数
XVar<-XHensaSqSum/(Xlen-1) # 分散
XHensa # 平均との偏差
XHensaSq # 偏差の2乗
XHensaSqSum # 偏差の2乗和
Xlen # データの個数
XVar # 分散
# 方法3
var(XYmatrix[,1]) # 身長の分散を求める
## 3.3. 便利な関数: seq(), rep()
seq(1:10) # 1から10まで10個の要素のベクトルを生成(1つずつ順に))
seq(10,100,10) # 10から100まで10飛ばしで10個の要素のベクトルを生成
rep(3,8) # 3を8回繰り返す
3:7 # 3から7までを順に表示
rep(3:7,3) # {3,4,5,6,7}のベクトルを3回繰り返す