PCA_DS07_1d
Hayashi Atsuhiro
2020/11/10
1. 先週のショート課題から: 10名
- 性別を分離すると正規性は確保しやすくなっていることが判ったであろうか?
-
R および RStudioの使い方は習得されたようですね。一部出力の取り込みに苦労されている方が見受けられますが、お困りならご連絡ください。
- QQプロットについてもう少し詳しく教えてください。: 後述
77. 前準備(Rの場合)
回帰分析の時と同様に、この後のことを考えて、欠損値を除外した変数を予め作っておこう。 今回は、身長と体重のデータをStuHWとし、それに胸囲を加えたデータをStuHWCとする。 以下の出力から判る通り、元のデータは494サンプルだったが、 StuHWは438サンプル、StuHWCは157サンプルである。 変量が多くなると欠損値を含むサンプルが多くなり、 分析対象とするデータのサンプル数が減る傾向にある。
# データ切り出し
dim(Student20c)## [1] 494 8StuHW<-na.omit(Student20c[,2:3]) # 欠損値を含むデータを削除
dim(StuHW)## [1] 438 2# colnames(StuHW)
StuHW[1:5,]## Height Weight
## 1 145.0 38
## 2 146.7 41
## 3 148.0 42
## 4 148.0 43
## 6 149.0 45StuHWC<-na.omit(Student20c[,2:4]) # 欠損値を含むデータを削除
dim(StuHWC)## [1] 157 3# colnames(StuHWC)
StuHWC[1:5,]## Height Weight Chest
## 2 146.7 41.0 85
## 4 148.0 43.0 80
## 7 150.0 46.0 86
## 11 151.7 41.5 80
## 12 152.0 35.0 772. 主成分分析
いくつか(p個)の変量の値を情報の損失をできるだけ少なくして、 少数変量(m個、m<p)の総合的指標(主成分)で代表させる方法として 主成分分析(Principal Component Analysis, PCA)と 因子分析(Factor Analysis, FA)がある。 いくつかのテストの成績を総合した総合的成績、 いろいろな症状を総合した総合的な重症度、 種々の財務指標に基づく企業の評価 等を求めたいといった場合に用いられる。 p変量(p次元)の観測値をm個(m次元)の主成分に縮約させるという意味で、 次元を減少させる(reduce)方法と言うこともでき、 多変量データを要約する有力な方法である。
両者は似た目的に使われるが、元になっている考え方は異なるので 利用する場面では注意が必要である。違いに焦点を当てながら説明する。 今回は主成分分析を取り上げ、次回因子分析を取り上げる。
3. 2変量の場合の主成分分析 : 理解を助けるため
-
定式化 :
-
変数 :
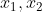
-
重み(係数) :
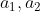
-
合成変量(線形結合) :
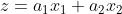
-
「よく代表する」ように、
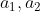 を決める。
を決める。
-
より広がって測定できる軸に沿うと情報量が多い。===> 広がり ===> 分散を最大に
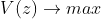 (制約条件 :
(制約条件 : 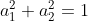 の下で)
の下で)なお、
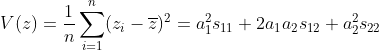 。
。
ただし、
[参考:立体の測定: イメージとして]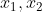 の分散を
の分散を 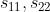 、共分散を
、共分散を 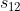 とする。
とする。- ノギスの使い方と寸法の読み取り方: 【通販モノタロウ】
- ノギス :ウィキペディア(Wikipedia)
-
全測定値の分散を最大化する身長と体重(
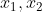 )の総合指標
)の総合指標 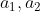 を求めよう。
を求めよう。
- 求まったベクトルを「軸」とか「主成分」と呼ぶ。
-
変数 :
-
出力結果 :
- Importance of components: 各軸の標準偏差(Standard deviation, 固有値の平方根)、比率(寄与率, Proportion of Variance, 全体に占める各軸の重み)、累積寄与率(Cumulative Proportion, 前者の累積和) : 軸ごとの重みの解釈に使う
-
各軸ごとに
-
固有ベクトル(係数
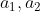 ) : 変量の特長の解釈に使う
) : 変量の特長の解釈に使う
- 主成分得点 : 各個人の得点(z)
-
固有ベクトル(係数
- 身長と体重の散布図
-
第1軸と第2軸の主成分得点(合成変数)の散布図(x軸が第1軸)
- 各変量の平均値
- 計算結果に対して、主成分得点 $x、標準偏差 $sdev(固有値の正の平方根)、$rotation (各主成分軸の固有ベクトル)、$center (解析に用いた各項目の値の平均) 等が格納される.
# 主成分分析(2変量) PCAresultHW<-prcomp(StuHW, scale=F) # 分散共分散行列に基づく # 分析結果要約 summary(PCAresultHW)## Importance of components: ## PC1 PC2 ## Standard deviation 11.2193 4.8813 ## Proportion of Variance 0.8408 0.1592 ## Cumulative Proportion 0.8408 1.0000◎主成分軸の固有ベクトル(各軸の特長を把握する)と回転の中心店の座標。
PCAresultHW$rotation## PC1 PC2 ## Height 0.5962119 0.8028271 ## Weight 0.8028271 -0.5962119PCAresultHW$center## Height Weight ## 169.30411 59.56621◎主成分得点(合成変数z)の先頭10ケースを表示させてみる。
PCAresultHW$x[1:10,]## PC1 PC2 ## 1 -31.80434 -6.653968 ## 2 -28.38230 -7.077798 ## 3 -26.80439 -6.630334 ## 4 -26.00157 -7.226546 ## 6 -23.79970 -7.616143 ## 7 -22.40066 -7.409528 ## 8 -22.60728 -6.010489 ## 9 -21.80445 -6.606700 ## 10 -18.59314 -8.991548 ## 11 -24.99982 -3.361768◎仕組みを理解してもらうために元データの散布図と、主成分得点(合成変数)のデータの散布図を描いてみる。
summary(StuHW)## Height Weight ## Min. :145.0 Min. : 35.00 ## 1st Qu.:165.0 1st Qu.: 53.00 ## Median :170.0 Median : 60.00 ## Mean :169.3 Mean : 59.57 ## 3rd Qu.:175.0 3rd Qu.: 65.00 ## Max. :187.0 Max. :100.00plot(StuHW[,2],StuHW[,1]) abline(v=seq(40,100,10), lty=3) abline(h=seq(150,180,10), lty=3) abline(h=169.3, lty=1) abline(v=59.6, lty=1)plot(PCAresultHW$x[,1], PCAresultHW$x[,2]) abline(h=seq(-20,10,5), lty=3) abline(v=seq(-30,40,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)# 別表記(何も指定をしないと第1軸と第2軸を描画) plot(PCAresultHW$x) abline(v=seq(-30,400,10), lty=3) abline(h=seq(-20,10,5), lty=3) abline(v=0, lty=1) abline(h=0, lty=1)◎ちょっと検算してみましょうか。求められた
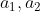 を用いてそれぞれの軸の主成分得点が計算できていることを確認せよ。
を用いてそれぞれの軸の主成分得点が計算できていることを確認せよ。StuHW_PCA<-cbind(StuHW, PCAresultHW$x) # 列側に連結(結合) StuHW_PCA[1:10,]## Height Weight PC1 PC2 ## 1 145.0 38.0 -31.80434 -6.653968 ## 2 146.7 41.0 -28.38230 -7.077798 ## 3 148.0 42.0 -26.80439 -6.630334 ## 4 148.0 43.0 -26.00157 -7.226546 ## 6 149.0 45.0 -23.79970 -7.616143 ## 7 150.0 46.0 -22.40066 -7.409528 ## 8 151.0 45.0 -22.60728 -6.010489 ## 9 151.0 46.0 -21.80445 -6.606700 ## 10 151.0 50.0 -18.59314 -8.991548 ## 11 151.7 41.5 -24.99982 -3.361768PCAresultHW$center # 回転の中心点## Height Weight ## 169.30411 59.56621PCAresultHW$rotation # 各軸の重み## PC1 PC2 ## Height 0.5962119 0.8028271 ## Weight 0.8028271 -0.5962119例えば、1番目のサンプルの主成分得点は、
第1軸(PC1): -31.8=(145.0-169.3)x0.596+(38.0-59.6)x0.803。
第2軸(PC2): -6.7=(145.0-169.3)x0.803+(38.0-59.6)x(-0.596)。◎散布図でも確かめてみよう。理解を促進するために本来の丸マークではなく、データ番号で散布図を描く。 元データは身長順、体重順に並べ替えてあり、主成分得点の小さいものが第1軸の左方向に位置していることが理解できる。 なお、回帰分析時にも話題になった体重が重い5サンプルが右下に位置している。
plot(StuHW_PCA[,3], StuHW_PCA[,4], type="n") # マークを描かない text(StuHW_PCA[,3], StuHW_PCA[,4]) # その場所に番号を表示 abline(h=seq(-20,10,5), lty=3) abline(v=seq(-30,40,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1) -
解釈方法
-
寄与率(Proportion of Variance) : その軸がどの程度説明力を持っているか :
- 第1軸だけで十分(84.1%)。第2軸に含まれる説明力は小さい(15.9%)。
-
固有ベクトル($rotation) : その軸の特徴を示している :
- 身長と体重の重みはほぼ同等(0.6と0.8)だが、体重がやや大きめに効いている(第1軸)
-
主成分得点と散布図 : 各個人がどこに付置されているか
- 第1軸 : 全体的な体格の指標。身長と体重を足したような指標。
- ちなみに第2軸 : 全体的な体格の指標だが、体重が負に効く。
-
元の散布図が回転していることが判るであろうか?
- 回転の中心点はそれぞれの変量の平均値。
-
寄与率(Proportion of Variance) : その軸がどの程度説明力を持っているか :
4. 3変量以上の主成分分析
-
定式化 :
- 2変量の時の考え方を拡張したもの(p変量)
-
合成変量(線形結合) :
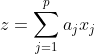
-
より広がって測定できる軸に沿うと情報量が多い。===> 広がり ===> 分散を最大に
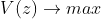 (制約条件 :
(制約条件 : 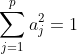 の下で)
の下で) -
合成変量の分散を最大化する軸を決定する。
-
よく代表するように、
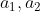 ,… を決める。
,… を決める。
-
身長、体重、胸囲での総合指標を求めてみよう :
-
出力結果 :
- Importance of components: 各軸の標準偏差(Standard deviation, 固有値の平方根)、比率(寄与率, Proportion of Variance, 全体に占める各軸の重み)、累積寄与率(Cumulative Proportion, 前者の累積和) : 軸ごとの重みの解釈に使う
-
各軸ごとに
-
固有ベクトル(係数
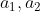 ,…) : 変量の特長の解釈に使う
,…) : 変量の特長の解釈に使う
- 主成分得点 : 各個人の得点(z)
-
固有ベクトル(係数
-
第1軸~第3軸の散布図
- 各変量の平均値
# 主成分分析(3変量) PCAresultHWC<-prcomp(StuHWC, scale=F) # 分散共分散行列に基づく # 分析結果要約 summary(PCAresultHWC)## Importance of components: ## PC1 PC2 PC3 ## Standard deviation 13.261 7.8672 5.01194 ## Proportion of Variance 0.669 0.2354 0.09556 ## Cumulative Proportion 0.669 0.9044 1.00000PCAresultHWC$rotation## PC1 PC2 PC3 ## Height 0.4940276 -0.4300973 -0.7556143 ## Weight 0.7486826 -0.2314239 0.6212225 ## Chest 0.4420534 0.8726163 -0.2076766PCAresultHWC$center## Height Weight Chest ## 168.96306 60.29745 85.87962PCAresultHWC$x[1:10,]## PC1 PC2 PC3 ## 2 -25.83507 13.273604 5.016950 ## 4 -25.90573 7.888548 6.315479 ## 7 -20.01931 11.569780 5.421859 ## 11 -25.20086 6.644324 2.587873 ## 12 -31.24524 5.401701 -1.053728 ## 17 -17.72083 11.036392 3.257950 ## 19 -15.33551 1.215742 10.407431 ## 24 -24.20554 0.541420 3.139153 ## 26 -17.37797 6.338597 3.509262 ## 31 -20.49193 9.042275 -1.389041# 別表記 # plot(PCAresultHWC$x) # abline(v=seq(-20,40,10), lty=3) # abline(h=seq(-50,10,10), lty=3) # abline(v=0, lty=1) # abline(h=0, lty=1) plot(PCAresultHWC$x[,1], PCAresultHWC$x[,2]) abline(h=seq(-50,10,10), lty=3) abline(v=seq(-30,40,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC$x[,2], PCAresultHWC$x[,3]) abline(h=seq(-10,20,5), lty=3) abline(v=seq(-50,10,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC$x[,3], PCAresultHWC$x[,1]) abline(h=seq(-25,40,10), lty=3) abline(v=seq(-10,20,5), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)◎理解を促進するために本来の丸マークではなく、データ番号で散布図を描く。
# 番号で描画してみる。 plot(PCAresultHWC$x[,1], PCAresultHWC$x[,2], type="n") # マークを描かない text(PCAresultHWC$x[,1], PCAresultHWC$x[,2]) # その場所に番号を表示 abline(h=seq(-50,10,10), lty=3) abline(v=seq(-30,40,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC$x[,2], PCAresultHWC$x[,3], type="n") # マークを描かない text(PCAresultHWC$x[,2], PCAresultHWC$x[,3]) # その場所に番号を表示 abline(h=seq(-10,20,5), lty=3) abline(v=seq(-50,10,10), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC$x[,3], PCAresultHWC$x[,1], type="n") # マークを描かない text(PCAresultHWC$x[,3], PCAresultHWC$x[,1]) # その場所に番号を表示 abline(h=seq(-25,40,10), lty=3) abline(v=seq(-10,20,5), lty=3) abline(h=0, lty=1) abline(v=0, lty=1) -
解釈方法
- 寄与率 : 2軸まで取れば十分のようだ(累積の項 90.4%)。
-
各軸の意味付け
- 第1軸 : 全体的な体格の因子。特に体重が効いている。
-
第2軸 : 太さの因子(?)。胸囲が正で大きく、身長が負。
- ちなみに第3軸 : 華奢さの因子(?)。無視しても良い軸であるが。(9.6%)。
5. 相関行列を使う理由
- 変量によって測定単位が異なる
- 使う単位によって解析結果が異なる
- 分散の影響を受ける
- 各変量を標準化して用いる : 相関行列 <===> 分散共分散行列
-
相関行列を用いて体格の総合指標を求めてみよう :
-
出力結果 :
- Importance of components: 各軸の標準偏差(Standard deviation, 固有値の平方根)、比率(寄与率, Proportion of Variance, 全体に占める各軸の重み)、累積寄与率(Cumulative Proportion, 前者の累積和) : 軸ごとの重みの解釈に使う
-
各軸ごとに
-
固有ベクトル(係数
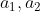 ,…) : 変量の特長の解釈に使う
,…) : 変量の特長の解釈に使う
-
固有ベクトル(係数
-
第1軸~第3軸の散布図
- 各変量の平均値
# 主成分分析(3変量, 相関行列を用いて) PCAresultHWC2<-prcomp(StuHWC, scale=T) # 相関行列に基づく(scale=Tがそのことを示す) # 分析結果要約 summary(PCAresultHWC2)## Importance of components: ## PC1 PC2 PC3 ## Standard deviation 1.3927 0.8787 0.53700 ## Proportion of Variance 0.6465 0.2574 0.09612 ## Cumulative Proportion 0.6465 0.9039 1.00000PCAresultHWC2$rotation## PC1 PC2 PC3 ## Height 0.5970039 -0.5045309 -0.6237266 ## Weight 0.6515461 -0.1486781 0.7438968 ## Chest 0.4680534 0.8504960 -0.2399637PCAresultHWC2$center## Height Weight Chest ## 168.96306 60.29745 85.87962# PCAresultHWC2$x[1:10,] # 別表記 # plot(PCAresultHWC2$x) # abline(h=seq(-5,1,1), lty=3) # abline(v=seq(-3,4,1), lty=3) # abline(h=0, lty=1) # abline(v=0, lty=1) plot(PCAresultHWC2$x[,1], PCAresultHWC2$x[,2]) abline(h=seq(-5,1,1), lty=3) abline(v=seq(-3,4,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC2$x[,2], PCAresultHWC2$x[,3]) abline(h=seq(-1,2.5,0.5), lty=3) abline(v=seq(-5,1,1), lty=3) abline(h=0, lty=1) abline(v=0, lty=1)plot(PCAresultHWC2$x[,3], PCAresultHWC2$x[,1]) abline(h=seq(-2,4,2), lty=3) abline(v=seq(-1,2.5,0.5), lty=3) abline(h=0, lty=1) abline(v=0, lty=1) -
解釈方法
- 寄与率 : 2軸まで取れば十分のようだ(累積の項 91.6%)。
-
各軸の意味付け
- 第1軸 : 全体的な体格の因子。
- 第2軸 : 太さの因子。
- 分散共分散行列を使ったときよりも第1軸の固有ベクトル同士が近い値になった。しかし、軸の解釈に違いはない。その理由はこの例では 3変量のスケールや分散にそれほどの違いがないためと想像される。
[演習1] 分散共分散行列と相関行列を使ったときの違いを見てみよう。身長のみを mm 単位で測定したと考えて、身長のみ10倍したデータを生成後、両者(分散共分散行列と相関行列)の出力を比較してみよ。
6. 主成分の数の決定基準
これでなければならないというようなルールが定まっているわけではないが、以下のような基準が一般的に 用いられている。また、結果の解釈の都合上、多少増減させることもある。
- 累積寄与率がある程度(例えば80%以上)以上大きくなること
- 固有値(標準偏差の2乗)のギャップがある程度以上大きいこと
- 相関行列を用いている場合、固有値が 1以上
- …
[ノウハウ] 軸の特性を把握するにはラインマーカーが重宝する。 一つの軸内で大きい(もしくは小さい)固有ベクトルにマークすると、 何がグルーピングされているかが理解し易くなる。 ただ、今週の例示では3軸までしか出現しないので、ご利益は感じにくいとも思う。 多変量(例えば以下の演習2)になればその有効性が理解できるであろう。
7. [演習2] 以下の食品の嗜好性データを分析してみよ。
100種類の食品(ごはん、お茶漬け、…、リンゴ、パイ缶)に対する 性・年齢で分割した10グループの嗜好度調査のデータをMoodleに掲載しておく。 グループ1から5は男性、グループ6から10は女性であり、その中の番号の小さい方から順に 15才以下、16~20才以下、21~30才以下、31~40才以下、41才以上の10群を構成している。 また、測定尺度は「1: おらく食べる気がしない」、「2: もし強制されれば食べる」、…、 「8: いつも食べたい」、「9: もっとも好きな食品に入る」までの9段階であり、 各グループごとに尺度の平均値を取ったものが測定値として格納されている。
なお、データのファイル名は「food.xlsx」(エクセル形式)であり、先頭18行には説明が入っているので 分析に供する際にはcsv形式に変換すると共にスキップする必要がある。 縦方向に100種類の食品が、横方向にグループが配置されている。 また、18行目にはグループ名が格納されている。
8. Q-Qプロットの説明
前回・前々回に回帰分析を取り上げた際に、残差の正規性を確認する方法の一つとしてQ-Qプロットを紹介した。 これをもう少し知りたいとの依頼があったので、動画を使って説明する。
この手法は、平均を0に、分散を1に標準化した2つの分布を比較するものであり、基準の分布を標準正規正規分布(平均0,分散1)として、 今回得られた残差の分布を対象分布として そのズレをプロットしたものである。 大まかな手順は以下の通り。 なお、確率側を比較するP-Pプロットもある。
- それぞれの分布を標準化する
- それぞれの分布の累積分布を作る
- 測定点の確率に対する正規分布の分位点を求める
- 両者を縦軸と横軸に取ってプロットする
- 全く同じ分布であれば、直線上にプロットされる
ちなみに、Qはquantile(分位点)、Pはprobability(確率)の頭文字を示している。
◎重回帰分析後のQ-Qプロット(再掲)
# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHWC$residuals)
qqline(RresultHWC$residuals, lty=2)
abline(h=seq(-10,30,10), lty=3) # 点線を追記
abline(h=0, lty=1) # 実線を追記
abline(v=0, lty=1) # 実線を追記88. 参考
このページで取り扱ったプログラムだけを抜き出して以下に列挙しておく。
# ディレクトリの移動。必須ではない。個々人の設定に応じて。
setwd("D:/home_sub3/R_Dir") # ホームディレクトリに移動(Set Working Directory)
## setwd("C:/home/R_Dir") # ホームディレクトリに移動(Set Working Directory)
getwd() # 現在のディレクトリ位置を表示
list.files() # ファイル・ディレクトリ一覧を表示
setwd("KougiDS") # ディレクトリを移動
list.files() # ファイル・ディレクトリ一覧を表示
# データの読み込み Ver.c=20年の2つのクラスのデータ
Student20c<-read.csv("StudAll20c.csv", skip=6,
header=TRUE, na.strings="NA")
dim(Student20c)
colnames(Student20c)
Student20c[1:5,]
# データ切り出し
dim(Student20c)
StuHW<-na.omit(Student20c[,2:3]) # 欠損値を含むデータを削除
dim(StuHW)
# colnames(StuHW)
StuHW[1:5,]
StuHWC<-na.omit(Student20c[,2:4]) # 欠損値を含むデータを削除
dim(StuHWC)
# colnames(StuHWC)
StuHWC[1:5,]
# 主成分分析(2変量)
PCAresultHW<-prcomp(StuHW, scale=F) # 分散共分散行列に基づく
# 分析結果要約
summary(PCAresultHW)
PCAresultHW$rotation
PCAresultHW$center
PCAresultHW$x[1:10,]
summary(StuHW)
plot(StuHW[,2],StuHW[,1])
abline(v=seq(40,100,10), lty=3)
abline(h=seq(150,180,10), lty=3)
abline(h=169.3, lty=1)
abline(v=59.6, lty=1)
plot(PCAresultHW$x[,1], PCAresultHW$x[,2])
abline(h=seq(-20,10,5), lty=3)
abline(v=seq(-30,40,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
# 別表記(何も指定をしないと第1軸と第2軸を描画)
plot(PCAresultHW$x)
abline(v=seq(-30,400,10), lty=3)
abline(h=seq(-20,10,5), lty=3)
abline(v=0, lty=1)
abline(h=0, lty=1)
StuHW_PCA<-cbind(StuHW, PCAresultHW$x) # 列側に連結(結合)
StuHW_PCA[1:10,]
PCAresultHW$center # 回転の中心点
PCAresultHW$rotation # 各軸の重み
plot(StuHW_PCA[,3], StuHW_PCA[,4], type="n") # マークを描かない
text(StuHW_PCA[,3], StuHW_PCA[,4]) # その場所に番号を表示
abline(h=seq(-20,10,5), lty=3)
abline(v=seq(-30,40,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
# 主成分分析(3変量)
PCAresultHWC<-prcomp(StuHWC, scale=F) # 分散共分散行列に基づく
# 分析結果要約
summary(PCAresultHWC)
PCAresultHWC$rotation
PCAresultHWC$center
PCAresultHWC$x[1:10,]
# 別表記
# plot(PCAresultHWC$x)
# abline(v=seq(-20,40,10), lty=3)
# abline(h=seq(-50,10,10), lty=3)
# abline(v=0, lty=1)
# abline(h=0, lty=1)
plot(PCAresultHWC$x[,1], PCAresultHWC$x[,2])
abline(h=seq(-50,10,10), lty=3)
abline(v=seq(-30,40,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC$x[,2], PCAresultHWC$x[,3])
abline(h=seq(-10,20,5), lty=3)
abline(v=seq(-50,10,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC$x[,3], PCAresultHWC$x[,1])
abline(h=seq(-25,40,10), lty=3)
abline(v=seq(-10,20,5), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
# 番号で描画してみる。
plot(PCAresultHWC$x[,1], PCAresultHWC$x[,2], type="n") # マークを描かない
text(PCAresultHWC$x[,1], PCAresultHWC$x[,2]) # その場所に番号を表示
abline(h=seq(-50,10,10), lty=3)
abline(v=seq(-30,40,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC$x[,2], PCAresultHWC$x[,3], type="n") # マークを描かない
text(PCAresultHWC$x[,2], PCAresultHWC$x[,3]) # その場所に番号を表示
abline(h=seq(-10,20,5), lty=3)
abline(v=seq(-50,10,10), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC$x[,3], PCAresultHWC$x[,1], type="n") # マークを描かない
text(PCAresultHWC$x[,3], PCAresultHWC$x[,1]) # その場所に番号を表示
abline(h=seq(-25,40,10), lty=3)
abline(v=seq(-10,20,5), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
# 主成分分析(3変量, 相関行列を用いて)
PCAresultHWC2<-prcomp(StuHWC, scale=T) # 相関行列に基づく(scale=Tがそのことを示す)
# 分析結果要約
summary(PCAresultHWC2)
PCAresultHWC2$rotation
PCAresultHWC2$center
# PCAresultHWC2$x[1:10,]
# 別表記
# plot(PCAresultHWC2$x)
# abline(h=seq(-5,1,1), lty=3)
# abline(v=seq(-3,4,1), lty=3)
# abline(h=0, lty=1)
# abline(v=0, lty=1)
plot(PCAresultHWC2$x[,1], PCAresultHWC2$x[,2])
abline(h=seq(-5,1,1), lty=3)
abline(v=seq(-3,4,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC2$x[,2], PCAresultHWC2$x[,3])
abline(h=seq(-1,2.5,0.5), lty=3)
abline(v=seq(-5,1,1), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)
plot(PCAresultHWC2$x[,3], PCAresultHWC2$x[,1])
abline(h=seq(-2,4,2), lty=3)
abline(v=seq(-1,2.5,0.5), lty=3)
abline(h=0, lty=1)
abline(v=0, lty=1)