2. 重回帰分析

　前回は構造がシンプルな単回帰分析を例に、この分析方法の考え方や残差の取り方、および、なぜそのように取る必要があるか等を説明した。今回は、より実用場面で登場する重回帰分析まで拡張し、分析の進め方や利用時の注意点を含めて紹介する。いろいろな場面での応用が可能な手法なので、大いに利用していただきたい。

2.1. 前準備(Rの場合)

　単回帰分析の時も説明したが、後々の分析(残差プロット)時に、データに欠損値が含まれていると計算できないので、分析対象の変量だけを事前に切り出して、欠損値を除外しておく。

　なお、今回もより多くのデータを収録した「StudAll20c.xlsx」をCSV形式に変換したデータ(StudAll20c.csv)を用いて説明を行うが、「前のデータのままで良い」という場合は、以下の「StudAll20c」を「StudAll20a」に読み替えて実行すれば良い。

# データ切り出し
dim(Student20c)

## [1] 494   8

StuHWC<-na.omit(Student20c[,2:4]) # 欠損値を含むデータを削除
dim(StuHWC)

## [1] 157   3

colnames(StuHWC)

## [1] "Height" "Weight" "Chest"

StuHWC[1:10,]

##    Height Weight Chest
## 2   146.7   41.0    85
## 4   148.0   43.0    80
## 7   150.0   46.0    86
## 11  151.7   41.5    80
## 12  152.0   35.0    77
## 17  153.0   46.5    87
## 19  153.0   55.0    78
## 24  154.4   44.0    75
## 26  155.0   48.0    83
## 31  156.0   42.0    85

元々の身長と体重のデータは494サンプルだったが、欠損値を含むデータが337サンプルあり、残ったのは157サンプルである。変量が多くなると欠損値を含むサンプルが多くなる傾向にある。以後は、Student20cの代わりにStudHWCを使って分析を行う。

2.2. 散布図行列

2変量のときには有用性が理解してもらえないと思ったので紹介しなかったが、 3変量以上の場合に変量間の関係を概観するのに便利な「散布図行列」を紹介しておく。 2変量ごとを組み合わせて散布図を行列形式で配置したものである。変量感でどの程度関係性がありそうかを視覚的に把握することができて便利である。

# 散布図行列
plot(StuHWC)

2.3. 重回帰分析 : 予測等に使う、連続変量の関係

2変量以上の説明する変量(説明変量)で 1変量(目的変量)を説明
説明変量が複数になる : 単 ===> 重
体重を身長と胸囲で説明(回帰)したい : [体重]=a+b[身長]+c[胸囲] : 回帰係数
- 説明される変量 : 目的変数、従属変数、dependent variable
- 説明する変量 : 説明変数、独立変数、independent variable
アイディアは単回帰分析の時と全く同じ。
- 関係性は直線＝線形を仮定する
- 回帰直線からのズレ(誤差)のことを回帰分析では「残差」と呼ぶ。
- 説明される変量(目的変量)と平行に残差を取る。なぜなら、指定された独立変数における測定誤差だから。
- 残差の分布は正規分布を仮定する
- 測定の場所によらず、残差は同一の分布であることを仮定する
- 残差の二乗和を最小にする(最小二乗法)
式の展開、解法。

直線の方程式:

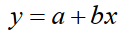
測定値と予測値のズレ:

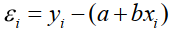
ズレの2乗の和を最小に:

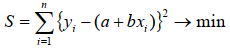
# 重回帰分析
RresultHWC<-lm(Weight~Height+Chest, data=StuHWC) # 右辺に説明する変量をプラスマークで追加していく

# 分析結果要約
summary(RresultHWC)

## 
## Call:
## lm(formula = Weight ~ Height + Chest, data = StuHWC)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -12.894  -3.868  -1.509   2.849  33.974 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -98.84919   12.07580  -8.186 9.56e-14 ***
## Height        0.77130    0.07213  10.694  < 2e-16 ***
## Chest         0.33565    0.06579   5.101 9.79e-07 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 7.223 on 154 degrees of freedom
## Multiple R-squared:  0.5384, Adjusted R-squared:  0.5324 
## F-statistic: 89.82 on 2 and 154 DF,  p-value: < 2.2e-16

2.4. 残差分析をお忘れなく

# 残差プロット
plot(StuHWC$Height, RresultHWC$residuals)  # 対身長
abline(v=seq(140,190,5), lty=3)     # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC$Chest, RresultHWC$residuals)  # 対胸囲
abline(v=seq(30,120,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC$Weight, RresultHWC$residuals)  # 対体重
abline(v=seq(30,100,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

残差の正規性を確かめてみよう。

残差のヒストグラム、箱ひげ図で偏りが判定できる。
残差のQQプロット

# 残差のヒストグラム
hist(RresultHWC$residuals, right=F)
abline(h=seq(0,150,25), lty=3)     # 点線を追記

# 残差の箱ひげ図
boxplot(RresultHWC$residuals, horizontal=T)
abline(v=seq(-10,30,10), lty=3)      # 点線を追記

# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHWC$residuals)
qqline(RresultHWC$residuals, lty=2)
abline(h=seq(-10,30,10), lty=3)   # 点線を追記
abline(h=0, lty=1)                # 実線を追記

Q-Q プロットの斜め直線に乗っていれば正規分布と言える。ズレが大きいようだと検討の余地がある。
程度問題ではあるが、少しぐらいの逸脱は許容範囲と言える。
残差が正規分布をするということを意識してもらえば良い。
[検討事項] 残差が20を超える辺りの4サンプルほどは(少なくとも)分布を乱しているように見える。===> 外れ値か? 吟味が必要。

2.5. 一部のサンプルを除外して分析してみよう

残差分析の結果、残差が20を超えている4サンプルについて吟味したところ、一般的な学生の体型と異なっていると判断し、これらを除外して分析をしてみよう。

元のExcelファイルに戻って除外する手もあるが、Rの中で実現するには、不等号や否定(!, Not)等をうまく組み合わせて、残差が20を超えるサンプルを除外する。それぞれの式の意味している事項が理解できるであろうか? もし理解できないようなら、式の中を分割して出力してみれば理解の促進になるであろう。

# 残差の大きいサンプルを抽出
StuResidOver20<-RresultHWC$residuals>20
RresultHWC$residuals[StuResidOver20]  # 20超えの残差一覧

##      231      340      341      428 
## 25.21708 33.97434 25.20585 23.96511

StuHWC[StuResidOver20,]               # 20超えのサンプル一覧

##     Height Weight Chest
## 231  169.3   88.5    94
## 340  173.0   84.0    46
## 341  173.0   90.0    90
## 428  178.0  100.0   112

20以下のサンプルの抽出。157サンプルから4サンプルを除外したので153サンプルになっている。以下では変数名をStuHWC2とした。

StuHWC2<-StuHWC[!StuResidOver20,]
StuHWC2[1:10,]

##    Height Weight Chest
## 2   146.7   41.0    85
## 4   148.0   43.0    80
## 7   150.0   46.0    86
## 11  151.7   41.5    80
## 12  152.0   35.0    77
## 17  153.0   46.5    87
## 19  153.0   55.0    78
## 24  154.4   44.0    75
## 26  155.0   48.0    83
## 31  156.0   42.0    85

dim(StuHWC2)

## [1] 153   3

では、抽出したデータ(153サンプル)を用いて改めて重回帰分析を行ってみよう。

# 重回帰分析
RresultHWC2<-lm(Weight~Height+Chest, data=StuHWC2)

# 分析結果要約
summary(RresultHWC2)

## 
## Call:
## lm(formula = Weight ~ Height + Chest, data = StuHWC2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.262  -3.502  -1.004   3.010  22.114 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -94.22920    9.66924  -9.745  < 2e-16 ***
## Height        0.71096    0.05774  12.314  < 2e-16 ***
## Chest         0.39223    0.05795   6.769 2.74e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.719 on 150 degrees of freedom
## Multiple R-squared:  0.6365, Adjusted R-squared:  0.6317 
## F-statistic: 131.3 on 2 and 150 DF,  p-value: < 2.2e-16

# 残差プロット
plot(StuHWC2$Height, RresultHWC2$residuals)  # 対身長
abline(v=seq(140,190,5), lty=3)     # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC2$Chest, RresultHWC2$residuals)  # 対胸囲
abline(v=seq(30,120,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC2$Weight, RresultHWC2$residuals)  # 対体重
abline(v=seq(30,100,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

残差の正規性を確かめてみよう。

残差のヒストグラム、箱ひげ図で偏りが判定できる。
残差のQQプロット

# 残差のヒストグラム
hist(RresultHWC2$residuals, right=F)
abline(h=seq(0,150,25), lty=3)     # 点線を追記

# 残差の箱ひげ図
boxplot(RresultHWC2$residuals, horizontal=T)
abline(v=seq(-10,30,10), lty=3)      # 点線を追記

残差のヒストグラム、箱ひげ図で偏りが判定できる。

# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHWC2$residuals)
qqline(RresultHWC2$residuals, lty=2)
abline(h=seq(-10,30,10), lty=3)   # 点線を追記
abline(h=0, lty=1)                # 実線を追記

2.6. この分析のまとめ(結果の見方)

対象になったのは 153名。
説明変量が予測に役立っているか?
- 回帰に役立っているか : p-value : 小さいと有意(役立っている)
決定係数 : Adjusted R-squared: ( 相関係数 : R )
- 目的変量が説明変量でどの程度説明しているかの割合。
- 1 に近いほど当てはまりが良いと言える。
回帰係数 : Estimate
説明変数が予測に役立っているか?
回帰係数の検定(係数=0 か?) : Pr(>|t|) : 小さいと有意(係数=0ではないと言える)
残差の性質 ===> 正規性 : 残差プロット、残差解析
- 残差(予測誤差)は正規分布をしていると仮定してモデルが構築されている。
- この仮定が覆ると、回帰分析として成立していないことになる。
- 残差が正規分布をしているか確認する必要がある。
- 均等に散らばっているか?
- 傾向はないか?
- …

# 分析結果要約 ＝ 再掲
summary(RresultHWC2)

## 
## Call:
## lm(formula = Weight ~ Height + Chest, data = StuHWC2)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -11.262  -3.502  -1.004   3.010  22.114 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -94.22920    9.66924  -9.745  < 2e-16 ***
## Height        0.71096    0.05774  12.314  < 2e-16 ***
## Chest         0.39223    0.05795   6.769 2.74e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.719 on 150 degrees of freedom
## Multiple R-squared:  0.6365, Adjusted R-squared:  0.6317 
## F-statistic: 131.3 on 2 and 150 DF,  p-value: < 2.2e-16

[参考: 出力の読み方の詳細] 統計検定のための、Rの出力結果からわかること（回帰分析編）

[演習1] 上述の重回帰分析について、残差が20を超える1サンプルは胸囲が異常に小さい。最初に気付くべきで今頃になってではあるが、入力ミスの可能性があるので、このサンプルを除外して再度分析してみよ。残差の分布や正規性はどのように変化したか確認せよ。

[演習2] 上述の重回帰分析について男性のみ、女性のみに分離して分析してみよ。

[演習3] 先週の単回帰分析について残差の大きいサンプルを除外して分析してみよ。

88. 参考

このページで取り扱ったプログラムだけを抜き出して以下に列挙しておく。

# ディレクトリの移動。必須ではない。個々人の設定に応じて。
setwd("D:/home_sub3/R_Dir")  # ホームディレクトリに移動(Set Working Directory)
## setwd("C:/home/R_Dir")  # ホームディレクトリに移動(Set Working Directory)
getwd()           # 現在のディレクトリ位置を表示
list.files()      # ファイル・ディレクトリ一覧を表示
setwd("KougiDS")  # ディレクトリを移動
list.files()      # ファイル・ディレクトリ一覧を表示
# データの読み込み Ver.c=20年の2つのクラスのデータ
Student20c<-read.csv("StudAll20c.csv", skip=6,
                     header=TRUE, na.strings="NA")
dim(Student20c)
colnames(Student20c)
Student20c[1:5,]

# データ切り出し
dim(Student20c)
StuHWC<-na.omit(Student20c[,2:4]) # 欠損値を含むデータを削除
dim(StuHWC)
colnames(StuHWC)
StuHWC[1:10,]

# 散布図行列
plot(StuHWC)

# 重回帰分析
RresultHWC<-lm(Weight~Height+Chest, data=StuHWC) # 右辺に説明する変量をプラスマークで追加していく

# 分析結果要約
summary(RresultHWC)

# 残差プロット
plot(StuHWC$Height, RresultHWC$residuals)  # 対身長
abline(v=seq(140,190,5), lty=3)     # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC$Chest, RresultHWC$residuals)  # 対胸囲
abline(v=seq(30,120,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC$Weight, RresultHWC$residuals)  # 対体重
abline(v=seq(30,100,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

# 残差のヒストグラム
hist(RresultHWC$residuals, right=F)
abline(h=seq(0,150,25), lty=3)     # 点線を追記
 
# 残差の箱ひげ図
boxplot(RresultHWC$residuals, horizontal=T)
abline(v=seq(-10,30,10), lty=3)      # 点線を追記

# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHWC$residuals)
qqline(RresultHWC$residuals, lty=2)
abline(h=seq(-10,30,10), lty=3)   # 点線を追記
abline(h=0, lty=1)                # 実線を追記

# 残差の大きいサンプルを抽出
StuResidOver20<-RresultHWC$residuals>20
RresultHWC$residuals[StuResidOver20]  # 20超えの残差一覧
StuHWC[StuResidOver20,]               # 20超えのサンプル一覧

StuHWC2<-StuHWC[!StuResidOver20,]
StuHWC2[1:10,]
dim(StuHWC2)

# 重回帰分析
RresultHWC2<-lm(Weight~Height+Chest, data=StuHWC2)

# 分析結果要約
summary(RresultHWC2)

# 残差プロット
plot(StuHWC2$Height, RresultHWC2$residuals)  # 対身長
abline(v=seq(140,190,5), lty=3)     # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC2$Chest, RresultHWC2$residuals)  # 対胸囲
abline(v=seq(30,120,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

plot(StuHWC2$Weight, RresultHWC2$residuals)  # 対体重
abline(v=seq(30,100,5), lty=3)      # 点線を追記
abline(h=seq(-10,30,10), lty=3)     # 点線を追記
abline(h=0, lty=1)                  # ゼロを実線で追記

# 残差のヒストグラム
hist(RresultHWC2$residuals, right=F)
abline(h=seq(0,150,25), lty=3)     # 点線を追記
 
# 残差の箱ひげ図
boxplot(RresultHWC2$residuals, horizontal=T)
abline(v=seq(-10,30,10), lty=3)      # 点線を追記

# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHWC2$residuals)
qqline(RresultHWC2$residuals, lty=2)
abline(h=seq(-10,30,10), lty=3)   # 点線を追記
abline(h=0, lty=1)                # 実線を追記

# 分析結果要約 ＝ 再掲
summary(RresultHWC2)

Reg_DS06_1f

Hayashi Atsuhiro

2020/11/02