Reg_DS05_1h
Hayashi Atsuhiro
2020/10/28
2. 回帰分析
今回は、多変量解析の代表的な手法である回帰分析について解説する。
工学系や農学系の実験等を行う領域では頻繁に使用される手法であるが、 日常的な話題の中でも概念は広く利用されているので、 取っ付き易い手法ではないだろうか。 過去のデータからその構造を把握し、新規に測定されたデータに対する予測を 行ないたいと言うときに、回帰分析は有用である。 構造のシンプルな単回帰分析でこの手法の原理を理解し、 複数の説明変量を用いた重回帰分析に拡張する。 残差の取り方や、その二乗和を最少にするという考えは同じである。
2.1. アイディア
散布図にもっともらしい「直線」を当てはめたい。
- 何に使う?
- 何に使える?
- 散布図: 縦軸=体重、横軸=身長
皆さんから収集した体格データを用いて、散布図を描いてみよう。どういう直線が「もっともらしい」と考えるか?
-
[注意] 散布図を丁寧に観るとデータの稠密な部分と疎な部分があることを理解せよ。
- どの様に直線の位置決めをすれば良い?
- 一意に決めるにはどの様なアイディアがある?
- そもそも、どういう考えから導き出された?
-
回帰分析とは?
- なぜ僕らは分布の中央付近を通過する直線が相応しいと感じるのか?
- それはどうやって決めたのか?
- 「誤差が一番小さい」直線が良さそうだ。
- では、その「誤差」って何? どう定義する?
-
また、「一番小さい」って何? どう定義する?
- ユニーク(唯一、一意)に決めるには何らかの定義が要るよね?
2.2. 前準備(Rの場合)
後々の分析(残差プロット)時に、データに欠損値が含まれていると計算できないので、分析対象の変量だけを切り出して、欠損値を除外しておく。
加えて、今回、新しいデータを提供する。 第3回の講義の中で、学生データとして「StudAll20a.xlsx」 (Excel形式)を提供したが、その後新しいデータが得られたので、 追加したものを「StudAll20c.xlsx」としてMoodleに置いておいた。 もし、より多くのデータを対象に演習がしたいと考えるのであれば、 Moodleからダウンロードし、CSV形式に変換して演習に供されたい。 以下では、そのデータ(StudAll20c.csv)を用いて話を進めるが、 「前のデータのままで良い」という場合は、 以下の「StudAll20c」を「StudAll20a」に読み替えて 実行すれば良い。若干計算結果は異なるが、 大きな違いはないので、理解の妨げになることはないと考えている。
# データの切り出し
colnames(Student20c)## [1] "Sex" "Height" "Weight" "Chest" "Residence"
## [6] "Remittance" "Carrier" "Fee"StudTmp1<-Student20c[,2:3] # 身長(2番目)と体重(3番目)だけを切り出す
StudTmp1[1:20,]## Height Weight
## 1 145.0 38.0
## 2 146.7 41.0
## 3 148.0 42.0
## 4 148.0 43.0
## 5 148.9 NA
## 6 149.0 45.0
## 7 150.0 46.0
## 8 151.0 45.0
## 9 151.0 46.0
## 10 151.0 50.0
## 11 151.7 41.5
## 12 152.0 35.0
## 13 152.0 43.0
## 14 152.0 44.0
## 15 153.0 41.0
## 16 153.0 42.0
## 17 153.0 46.5
## 18 153.0 50.0
## 19 153.0 55.0
## 20 153.0 NAdim(StudTmp)## [1] 494 8元々の身長と体重のデータは 494例だったが、欠損値を含むデータが56例あり、 残ったのは438例である。
StudHW<-na.omit(StudTmp1) # 欠損値を含むデータを削除
dim(StudHW)## [1] 438 2colnames(StudHW)## [1] "Height" "Weight"## RresultHW <- lm(Weight ~ Height, data=StudHW)
## RresultHW
## summary(RresultHW)以後は、Student20cの代わりにStudHWを使って分析を行う。
2.3. 単回帰分析 : 予測等に使う、連続変量の関係
- 体重を身長で説明(回帰)したい : [体重]=a+b[身長] : 回帰係数
- 関係性は直線=線形を仮定する
- 説明される変量 : 目的変数、従属変数、dependent variable
-
説明する変量 : 説明変数、独立変数、independent variable
- 誤差の取り方 : 指定された独立変数における測定誤差。だから誤差は垂直方向に分布する。
- 回帰直線からのズレ(誤差)のことを回帰分析では「残差」と呼ぶ。
- 残差の分布は正規分布を仮定する
- 測定の場所によらず、残差は同一の分布であることを仮定する
-
どうやって直線を決める? : 予測誤差の2乗和を最小にする
-
式の展開、解法。
直線の方程式:
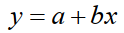
測定値と予測値のズレ:
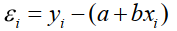
ズレの2乗の和を最小に:
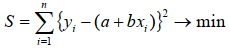
-
[余談] 回帰分析では「2乗和」を最小にすることを考えるが、「絶対値和」とか「符号付き和(1乗和)」を最小にする方法もアイディアとしてはあり得る。 2乗和だと式の展開が楽になる。
-
説明する変数の個数
- 一つ: 単回帰: 身長で説明したい
- 複数: 重回帰: 身長と胸囲で説明したい、…
# 表記方法 その1
Rresult1 <- lm(StudHW$Weight ~ StudHW$Height,
data=StudHW) # 線形モデル, Linear Model
Rresult1##
## Call:
## lm(formula = StudHW$Weight ~ StudHW$Height, data = StudHW)
##
## Coefficients:
## (Intercept) StudHW$Height
## -78.0283 0.8127summary(Rresult1)##
## Call:
## lm(formula = StudHW$Weight ~ StudHW$Height, data = StudHW)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.446 -4.446 -1.038 3.212 34.617
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -78.02833 7.39601 -10.55 <2e-16 ***
## StudHW$Height 0.81271 0.04364 18.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.072 on 436 degrees of freedom
## Multiple R-squared: 0.443, Adjusted R-squared: 0.4418
## F-statistic: 346.8 on 1 and 436 DF, p-value: < 2.2e-16# 表記方法 その2
RresultHW <- lm(Weight ~ Height,
data=StudHW) # 線形モデル, Linear Model
RresultHW##
## Call:
## lm(formula = Weight ~ Height, data = StudHW)
##
## Coefficients:
## (Intercept) Height
## -78.0283 0.8127summary(RresultHW)##
## Call:
## lm(formula = Weight ~ Height, data = StudHW)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.446 -4.446 -1.038 3.212 34.617
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -78.02833 7.39601 -10.55 <2e-16 ***
## Height 0.81271 0.04364 18.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.072 on 436 degrees of freedom
## Multiple R-squared: 0.443, Adjusted R-squared: 0.4418
## F-statistic: 346.8 on 1 and 436 DF, p-value: < 2.2e-16- 回帰直線の係数はそれぞれ -78.0と0.813と求められた。
- これを使えば、建物の入り口にメジャーを貼り付けておけば体重を言い当てられるはず。
-
[演習] 試しに自分の体重がうまく予測できているか計算してみよ。
- -78.0+0.813*179=67.5Kg。
- 残差は 90.6-67.5=23.1Kg。
- うーん、メタボ健診に引っかかるわけだ。
- 係数や残差を取り出して表示することもできる。
coef <-RresultHW$coefficient
resid<-RresultHW$residuals
coef # 回帰係数## (Intercept) Height
## -78.0283291 0.8127064resid[1:20] # 残差(先頭の20例)## 1 2 3 4 6 7
## -1.8141038 -0.1957047 -0.2522231 0.7477769 1.9350705 2.1223640
## 8 9 10 11 12 13
## 0.3096576 1.3096576 5.3096576 -3.7592369 -10.5030488 -2.5030488
## 14 15 16 17 18 19
## -1.5030488 -5.3157553 -4.3157553 0.1842447 3.6842447 8.6842447
## 22 23
## -0.7221085 -1.1284617- 散布図に回帰直線を付加する方法。
plot(Weight ~ Height, data=StudHW)
abline(RresultHW)
abline(h=seq(40,100,10), lty=3)
abline(v=seq(140,190,5), lty=3)2.4. 残差分析もお忘れなく
- 回帰直線の係数が求まったらそれでおしまい?
-
仮定が3つあったはず
- 関係性は直線=線形を仮定する
- 誤差の分布は正規分布を仮定する
- 測定の場所によらず、残差は同一の分布であることを仮定する
- 仮定が成り立っているかは確認せねば。どうやって?
# 残差プロット: 対身長に対して
plot(StudHW$Height, RresultHW$residuals)
abline(v=seq(140,190,5),lty=3) # 点線を追記
abline(h=seq(-10,30,10),lty=3) # 点線を追記
abline(h=0,lty=1) # 原点を追記# 残差プロット: 対体重に対して
plot(StudHW$Weight, RresultHW$residuals)
abline(v=seq(30,100,5),lty=3) # 点線を追記
abline(h=seq(-10,30,10),lty=3) # 点線を追記
abline(h=0,lty=1) # 原点を追記- もし、残差が何らかの傾向を示しているなら、直線=線形関係ではないのかもしれないと疑う必要がある。 ==> バナナカーブ
- 測定する場所で残差の傾向が異なるなら、残差の分布が同一とは言えないかもしれない。 ==> 順に広がっているラッパカーブ
# 残差のヒストグラム
hist(RresultHW$residuals, right=F)
abline(h=seq(0,150,25),lty=3) # 点線を追記# 残差の箱ひげ図
boxplot(RresultHW$residuals, horizontal=T)
abline(v=seq(-10,30,10),lty=3) # 点線を追記- 残差のヒストグラム、箱ひげ図で偏りが判定できる。
# 残差のQQプロット: 正規確率プロット
qqnorm(RresultHW$residuals)
qqline(RresultHW$residuals, lty=2)
abline(h=0,lty=1) # 点線を追記
abline(h=seq(-10,30,10),lty=3) # 点線を追記-
Q-Q プロットの斜め直線に乗っていれば正規分布と言える。ズレが大きいようだと検討の余地がある。
-
[検討事項] 残差が20を超える辺りの5例ほどは(少なくとも)分布を乱しているように見える。===> 外れ値か? 吟味が必要。
2.5. その他の情報
ここまでで回帰直線の当てはめに疑義がなければ、他に得られる情報についても知っておくと良い。
-
決定係数 : R-Square
Adjusted R-squared: 0.4418
F-statistic: 346.8 on 1 and 436 DF, p-value: < 2.2e-16
Estimate Std. Error t value Pr(>|t|)
(Intercept) -78.02833 7.39601 -10.55 <2e-16 ***
Height 0.81271 0.04364 18.62 <2e-16 ***
summary(RresultHW)##
## Call:
## lm(formula = Weight ~ Height, data = StudHW)
##
## Residuals:
## Min 1Q Median 3Q Max
## -15.446 -4.446 -1.038 3.212 34.617
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -78.02833 7.39601 -10.55 <2e-16 ***
## Height 0.81271 0.04364 18.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 7.072 on 436 degrees of freedom
## Multiple R-squared: 0.443, Adjusted R-squared: 0.4418
## F-statistic: 346.8 on 1 and 436 DF, p-value: < 2.2e-162.6. この分析のまとめ(結果の見方)
-
対象になったのは 438名。
-
説明変量が予測に役立っているか?
-
回帰に役立っているか : p-value : 小さいと有意(役立っている)
-
[この例] 1% 未満(0.01%) なので役に立っていると言える。
-
回帰に役立っているか : p-value : 小さいと有意(役立っている)
-
決定係数 : Adjusted R-squared: ( 相関係数 : R )
- 目的変量が説明変量でどの程度説明しているかの割合。
-
1 に近いほど当てはまりが良いと言える。
-
[この例] 44% 程(約半分)を説明できている。
-
回帰係数 : Estimate
-
[この例] a=-78.0, b=0.813
-
説明変数が予測に役立っているか?
回帰係数の検定(係数=0 か?) : Pr(>|t|) : 小さいと有意(係数=0ではないと言える)-
[この例] 両者とも 1% 未満(0.01%) なので回帰係数はゼロではない(何らかの意味がある数字と言える)。
-
残差の性質 ===> 正規性 : 残差プロット、残差解析
- 残差(予測誤差)は正規分布をしていると仮定してモデルが構築されている。
- この仮定が覆ると、回帰分析として成立していないことになる。
- 残差が正規分布をしているか確認する必要がある。
- 均等に散らばっているか?
- 傾向はないか?
-
…
[この例] 残差には概ね傾向は見られない。 ただし体重の大きい 5例程度は要確認。場合によっては外れ値として除外も。
[演習] 上述では[体重]を[身長]で説明する回帰式の例で説明した。では、[体重]を[胸囲]で説明するとどうなるか? 各自でやってみよ。
2.7. 改めて注意事項
-
誤差は「説明変量」の軸と垂直に取ることに注意せよ。 誤差は測定時に混入していると考えてモデルが構築されているから。
-
幾つかのチェック項目
- 残差に一様性があるか? 残差プロット
- 残差が正規性をしているか? 診るには? Q-Q plot
-
有効桁数に注意せよ : どこまでが「意味ある桁」か?
[例1] 四捨五入の数値で考えてみれば : 精度(正確さ)が異なることに注意
測定精度上回る計算結果は出せても、意味はない。 プログラムの出力をそのまま書き写さないように。
[重要な注意] 統計ソフトは単なる道具。使いこなすのは各自。-
12.3 <=== 12.25~12.34
12 <=== 11.5 ~12.467.8 <=== 67.75~67.84
68 <=== 67.5 ~68.4[例2] 日本の観測史上の最高気温は、 2018(平成30)年7月23日に熊谷市で観測された41.1度であり、 最低気温は、1902(明治35)年1月25日に北海道旭川市の-41度であった。===> -41.0度
[例3] 2001年のイチロー選手の打率は3割5分であった。 2006年は3割3分1厘であった。===> 3割5分0厘